Graphenalgorithmen anschaulich dargestellt

Graphen sind ein häufig genutztes Werkzeug zur Modellierung von strukturellen Zusammenhängen. Sie bestehen aus Knoten, die durch Kanten miteinander verbunden sein können (gerichtet und / oder ungerichtet). Hier sind einige wichtige Anwendungen von Graphen:

Routenplanung: Hier repräsentieren die Knoten wichtige Orte (Städte, Kreuzungen), die Kanten stellen verbindende Straßen dar. Einbahnstraßen können durch eine gerichtete Kante modelliert werden.
Kommunikationsnetzwerke: Die Knoten repräsentieren hier Telefone, Modems, Server, Service Provider oder andere Kommunikationsgeräte und -teilnehmer, die Kanten stehen für Datenleitungen, die diese miteinander verbinden.
Gantt-Diagramme für die Ablaufplanung: Die einzelnen Stufen eines Projekts werden durch Konten dargestellt, gerichtete Kanten repräsentieren Abhängigkeiten zwischen diesen Phasen.
Darstellung hierarchischer Strukturen: Die Knoten können hier Arbeitnehmer oder Abteilungen darstellen während die Kanten für Ordnungsbeziehungen (Vorgesetzte / Untergebene) stehen.

Der Umgang mit solchen Modellen ist ein wichtiges Hilfsmittel in der Mathematik und in der Informatik. Viele grundlegende Algorithmen basieren auf Graphenmodellen, einige davon stellen wir im Folgenden vor. Neben einer Erklärung und dem Pseudocode gibt es auch ein interaktives Applet, um die Algorithmen auf eigenen Beispielen ausprobieren und erforschen zu können.

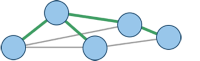
Minimale Spannbäume

Ein Spannbaum ist eine Teilmenge der Kanten eines Graphen, die alle Knoten miteinander verbindet, aber möglichst wenige Kanten enthält. Die Frage nach einem Spannbaum (meistens nach einem mit möglichst geringen Kosten) taucht oft in Kommunikationsnetzen auf. Hier ist es wichtig, dass jeder Knoten (Teilnehmer) mit jedem anderen kommunizieren kann (möglicherweise über Umwege). Ein anderer Anwendungsfall sind Versorgungs- und Verteilnetze (beispielsweise Wasserversorgung, Stromnetze).

Algorithmen: Algorithmus von Prim, Algorithmus von Kruskal

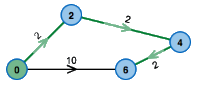
Kürzeste Wege

Eine der häufigsten Anwendungen von Graphen im Alltag ist die Darstellung von Infrastruktur- und Kommunikationsnetzen. Man denke beispielsweise an Straßenkarten, Buslinienpläne oder Flugverbindungen, all diese Dinge können durch Graphen repräsentiert werden.

Die Frage nach einem Weg zwischen zwei gegebenen Knoten in solchen Graphen ist eine besonders wichtige Anwendung. Meistens geht es dabei um ‘kostengünstige’ Wege, wobei ‘kostengünstig’ durchaus verschiedene Bedeutungen haben kann. Vielleicht such man nach dem kürzesten oder schnellsten Weg, vielleicht nach dem mit dem geringsten Energieverbrauch, den geringsten Reisekosten oder auch dem, der am wenigsten Geschwindigkeitskontrollen enthält.

Algorithmen: Floyd-Warshall-Algorithmus, Algorithmus von Dijkstra, Bellman-Ford-Algorithmus, A*-Algorithmus

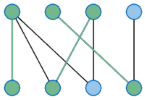
Matchings

Das Matching-Problem fragt nach einer Zuordnung zwischen den Elementen von verschiedenen (häufig zwei) Mengen. Ein klassisches Beispiel ist das sogenannte ‘Heiratsproblem’: Gegeben sind eine Menge von Frauen und eine Menge von Männern, die alle heiratswillig sind. Bekannt ist außerdem, wer jeweils welchen Partner akzeptieren würde. Ein Matching besteht dann in der Bildung von Paaren, die alle ‘miteinander kompatibel’ sind, also bereit sind, einander zu heiraten. Das gewichtete Matching-Problem ist ein allgemeinerer Fall, der außerdem noch Bewertungen enthält, die angeben, welche Paarungen jeweils bevorzugt werden. Dieses Problem kann durch die Ungarische Methode gelöst werden.

Algorithmen: Blossom-Algorithmus, Hopcroft-Karp Algorithmus, Ungarische Methode

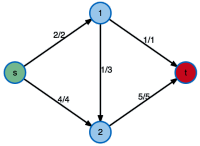
Flüsse in Netzwerken

In Graphen und Netzwerken trifft man häufig auf die Problemstellung, einen Fluss zu bestimmen. Dabei kann es sich um einen Güterfluss durch ein Logistiknetz handeln, um Informationen, die in einem Kommunikationsnetzwerk zwischen den Teilnehmerinnen und Teilnehmern ausgetauscht werden, oder um den Transport von Erdgas in einem Versorgungsnetz. Meist ist das Ziel die Bestimmung eines maximalen Flusses zwischen zwei gegebenen Knoten, wobei die Kapazität jeder einzelnen Kante beschränkt ist. Oft ist man auch daran interessiert, eine vorgegebene Flussmenge möglichst kostengünstig von einem Start- zu einem Zielkonten zu transportieren, man sucht also einen Fluss mit minimalen Kosten.

Algorithmen: Cycle-Cancelling-Methode, Ford-Fulkerson-Algorithm

Routenplanung

Ein klassisches Problem der Graphentheorie ist Eulersche Pfadproblem: Bestimme einen Pfad oder Kreis durch den Graphen, der jede Kante genau einmal benutzt. Eine erste Formulierung dieser Fragestellung ist als Königsberger Brückenproblem bekannt: ‘Der Fluss Pregel trennt die Stadt Königsberg (heute Kaliningrad) in fünf Teile die durch sieben Brücken miteinander verbunden sind. Gibt es einen Rundweg durch Königsberg, bei dem man jede Brücke genau einmal überquert?’

Beim verwandten Chinese Postman-Problem geht es darum, einen möglichst kurzen Weg in einem Graphen zu finden, der jede Kante (gerichtet oder ungerichtet) mindestens einmal verwendet und dann zum Ausgangspunkt zurückkehrt. Dieses Problem ist etwa für einen Postboten wichtig, der Briefe in einer Stadt austrägt und daher jede Straße entlanglaufen muss. Das Problem des Handlungsreisenden zielt darauf ab, eine möglichst kurze Rundreise durch alle Knoten eines Graphen zu finden.

Algorithmen: Problem des Handlungsreisenden, Algorithmus von Hierholzer, Chinese Postman-Problem