Matchings

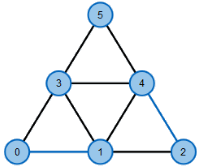
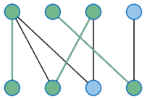
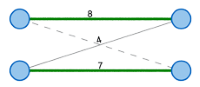
Das Matching-Problem fragt nach einer Zuordnung zwischen den Elementen von verschiedenen (häufig zwei) Mengen. Ein klassisches Beispiel ist das sogenannte ‘Heiratsproblem’: Gegeben sind eine Menge von Frauen und eine Menge von Männern, die alle heiratswillig sind. Bekannt ist außerdem, wer jeweils welchen Partner akzeptieren würde. Ein Matching besteht dann in der Bildung von Paaren, die alle ‘miteinander kompatibel’ sind, also bereit sind, einander zu heiraten. Das gewichtete Matching-Problem ist ein allgemeinerer Fall, der außerdem noch Bewertungen enthält, die angeben, welche Paarungen jeweils bevorzugt werden. Dieses Problem kann durch die Ungarische Methode gelöst werden.