Tour durch 107 Städte Deutschlands Kürzeste Rundtouren: Das Problem des Handlungsreisenden Technische Universität München

Kürzeste Rundtouren

Willkommen zum TSP-Spiel!

Auf dieser Seite geht es um das sogenannte "Problem des Handlungsreisenden" oder auch "Traveling Salesman Problem".

Dieses Problem beschäftigt sich mit der Frage, wie man eine Tour durch eine bestimmte Anzahl Städte und zurück zum Ausgangspunkt planen muss, damit der insgesamt zurückgelegte Weg möglichst klein ist. Sie ist beispielsweise für vier Städte sehr leicht zu beantworten, doch bereits bei zehn Städten sind potenziell 181.440 verschiedene solcher Rundtouren möglich.

Wie schafft man es also, zwanzig oder noch mehr Städte auf dem kürzesten Weg zu besuchen?

Zu diesem Zweck wurden in den letzten Jahrzenten verschiedene Algorithmen entwickelt, die das Problem des Handlungsreisenden möglichst schnell beantworten.

Doch jetzt bist du am Zug!

Erstelle im nächsten Tab ein Spiel und versuche selbst, die kürzeste Rundtour zu finden! Anschließend kannst du dir die Lösung, sowie die Berechnungsschritte der verwendeten Algorithmen ansehen.

Viel Spaß!

Was möchtest du zuerst tun?

Tour durch 107 Städte Deutschlands

Neues Spiel

Karte:



Metrik:

Spiel wiederholen

Game Code:
Fehler

    Hier kannst du ein Spiel erstellen!

    Wähle dazu eine Karte und die Anzahl der Städte, die besucht werden sollen. Falls deine Wahl auf die Karte "Grid" gefallen ist, kannst du dir anschließend eine aus drei verschiedenen Metriken aussuchen. Sie gibt an, wie Distanzen zwischen zwei Städten berechnet werden sollen:
    Euklidsche Metrik Euklidsche Metrik
    √ (x1-x2)2 + (y1-y2)2 
    Eins-Metrik Euklidsche Metrik
    |x1-x2|+|y1-y2|
    Maximum-Metrik Euklidsche Metrik
    max{|x1-x2|,|y1-y2|}
    Ihr Browser unterst¨tzt kein HTML5 Canvas. Bitte verwenden Sie einen modernen Browser, z.B.Mozilla Firefox

    Länge deiner Tour:

    0 km

    Zeichne deine Tour!

    Zeichne hier deine Rundtour ein!
    Sie soll möglichst kurz sein, muss aber alle Städte besuchen.
    Per Rechts- oder Doppelklick kannst du bereits gezeichnete Wege wieder löschen. Ausgefüllte Städte wurden bereits besucht und anschließend wieder verlassen.

    Lasse dir die Lösung anzeigen!

    Sobald du alle Städte besucht hast, kannst du dir hier eine optimale Tour anzeigen lassen, die du mit deiner eigenen Lösung vergleichen kannst. Möchtest du die Lösung sofort sehen, drücke in der Tableiste auf "Optimale Tour".
    Du besuchst nicht alle Knoten!
    Deine Tour enthält Subtouren!

    Spiele dieses Spiel erneut!

    Um das aktuelle Spiel zu einem späteren Zeitpunkt erneut zu spielen, kannst du dir hier den GameCode anzeigen lassen und diesen beim Erstellen des Spiels unter "Spiel wiederholen" eingeben.
    GameCode einblenden...

    Teste deine logistischen Fähigkeiten und zeichne eine möglichst kurze Rundtour.

    Vergiss dabei nicht, jede Stadt genau einmal zu besuchen.

    Mit dem Wechsel des Tabs wird das Zeichnen der Tour beendet.

    Es ist danach nicht mehr möglich, in den Spieltab zurückzukehren.

    Ihr Browser unterstützt kein HTML5 Canvas. Bitte verwenden Sie einen modernen Browser, z.B.Mozilla Firefox

    Länge der optimalen Tour:

    0 km

    Länge deiner Tour:

    0 km

    Berechnungszeit:

    0 ms

    Glückwunsch! Deine Tour ist optimal.

    Schade! Deine Tour ist leider nicht optimal.

    Schade! Deine Tour besucht leider nicht alle Knoten.

    Schade! Deine Tour enthält leider Subtouren.

    Wie wurde die Lösung berechnet?

    Mit Klick auf den Button erhältst du nähere Informationen zur Funktionsweise der verwendeten Algorithmen, die zur Findung der Lösung beigetragen haben.
    Du kannst dir aber auch direkt die Berechnungsschritte anzeigen lassen, die zu dieser Rundtour geführt haben.
    GameCode einblenden...

    Glückwunsch! Deine Tour ist optimal.

    Schade! Deine Tour ist leider nicht optimal.

    Schade! Deine Tour besucht leider nicht alle Knoten.

    Schade! Deine Tour enthält leider Subtouren.

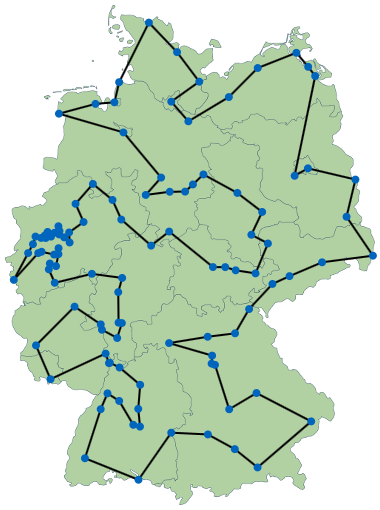
    Optimale Tour:
    Deine Tour:

    Hier kannst du dir die optimale Tour und die dazugehörigen Berechnungsschritte ansehen.

    In der Beschreibung des Algorithmus findest du genauere Informationen zu den verwendeten Algorithmen der einzelnen Schritte.

    Schaue dir hier an, wie die verschiedenen Algorithmen funktionieren. Klicke dazu auf den Namen des gewünschten Algorithmus.

    Graphen und Algorithmen

    Die Punkte auf der Karte des Spiels symbolisieren Städte. Eine Linie zwischen zwei Städten stellt die kürzeste Verbindung zwischen ihnen dar. Man kann diese Objekte aber auch abstrakter ausdrücken.
    In der sogenannten Graphentheorie heißen Punkte "Knoten" und Linien nennt man "Kanten". Eine Ansammlung solcher Knoten und Kanten heißt "Graph", er ist gewissermaßen die Landkarte.
    Wenn wir im Zusammenhang mit dem Traveling Salesman Problem von Algorithmen sprechen, unterscheiden wir grundsätzlich zwei Arten:
    • "Heuristiken", die eine Rundtour finden, von der aber nicht bekannt ist, wie gut sie im Verhältnis zu einer optimalen Lösung ist. Ihre Länge ist auf jeden Fall größer als die der optimalen Lösung. Man nennt die Länge der gefundenen Tour dann "obere Schranke".
    • "Exakte Lösungsverfahren", die sich langsam einer optimalen Rundtour annähern. Ihre gefundenen Wege sind nie länger als eine optimale Lösung. Deshalb bezeichnet man ihre Länge als "untere Schranke". Ihr Ergebnis stellt in den wenigsten Fällen eine Rundtour durch alle Knoten dar.
    Man weiß also, dass die Länge einer kürzesten Rundtour zwischen diesen beiden Schranken liegen muss. Je besser die Verfahren sind, desto kleiner wird der Abstand zwischen den Schranken und desto genauer kann man die Länge einer optimalen Lösung angeben.

    Nearest-Neighbor-Heuristik

    Will man den Nearest-Neighbor-Algorithmus beschreiben, versetzt man sich einfach in seine Lage. Dazu wählt man zunächst einen Startknoten aus, von dem aus die Reise losgehen soll.
    Wie der Name dieser Methode bereits verrät, gehen wir nun zu dem Knoten, der unserer aktuellen Position am nächsten liegt. Wir legen also den kürzesten Weg zurück, den wir finden können. Natürlich dürfen wir nur Knoten ansteuern, die wir auf unserer Rundtour noch nicht besucht haben.
    Diesen Schritt wiederholen wir so lange, bis kein Knoten mehr übrig ist. Dann kehren wir zum Startknoten zurück.
    Obwohl es im ersten Moment so scheint, als könnte man auf diese Weise immer eine kürzeste Rundtour finden, ist das nicht der Fall. Dass eine solche Tour nur selten optimal ist, lässt sich sehr schön im Berechnungsschritte-Tab sehen. Dort wird der Nearest-Neighbor-Algorithmus gleich als erstes auf den Graphen angewendet.

    Multiple-Fragment-Heuristik

    Mithilfe der Multiple-Fragment-Heuristik wird die Rundtour "Stück für Stück" zusammengesetzt, vergleichbar mit einem Puzzle. Dazu sortieren wir die Kanten des Graphen ihrer Länge nach. Jetzt fügen wir, beginnend mit der kürzesten, nacheinander Kanten zwischen den Städten ein.
    Dabei müssen wir zwei Punkte beachten:
    • An einem Knoten dürfen nicht mehr als zwei Kanten anliegen.
    • Es dürfen keine Kreise entstehen.
    Dadurch erhalten wir eine Rundtour.

    Lagrange-Relaxierung

    Die auf dieser Seite verwendete Lagrange-Relaxierung erweitert die Menge möglicher Lösungen um die sogenannten "minimalen Eins-Bäume". Bei einem Eins-Baum handelt es sich um einen Weg, der alle Knoten genau einmal besucht und anschließend durch Hinzufügen einer weiteren Kante genau einen Kreis erhält. Er wird minimal, wenn man zu seiner Erstellung nur die kürzesten Kanten benutzt. Anschließend wird die Länge der Kanten so modifiziert, dass das Ergebnis des nächsten Berechnungsschritts ein anderes ist.
    Sie funktioniert in groben Zügen folgendermaßen:
    • Entferne einen Knoten aus dem Graphen.
    • Füge zwischen den verbleibenden Knoten Kanten ihrer Länge nach ein, ähnlich dem Multiple-Fragment-Verfahren. Hier dürfen beliebig viele Kanten an einem Knoten anliegen, ein Kreis darf aber nicht entstehen.
    • Füge nun den zu Beginn entfernten Knoten wieder ein und mit ihm zwei kürzeste Kanten, die ihn "berühren". Haben wir dadurch eine Rundtour erhalten, hören wir auf. Es gibt keine kürzere Rundtour. Ansonsten machen wir weiter.
    • Unser Ziel ist es, dass an jedem Knoten genau zwei Kanten anliegen. Finde also zu jedem Knoten heraus, um wieviel sich die anliegende Kantenmenge von 2 unterscheidet. Berühren vier Kanten einen Knoten, erhält man als Ergebnis beispielsweise 2, ist es nur einer, erhält man -1. Addiere das Ergebnis zur Länge aller anliegenden Kanten.
    • Kehre jetzt zum ersten Schritt zurück.
    Da diese Methode unter Umständen sehr lange braucht, bis sie die optimale Lösung zurückgibt, kann es sinnvoll sein, sich zu überlegen, wann man die Berechnung abbrechen möchte.

    Branch-and-Bound

    Der Branch-and-Bound-Algorithmus knüpft direkt an die Lagrange-Relaxierung an. Konnte mithilfe letzterer keine Lösung gefunden werden, verkleinert man die Menge der möglichen Lösungen und führt sie auf der neuen Menge erneut aus.
    Dazu wählt man einen Knoten an dem in der letzten Lösung drei Kanten angelegen sind. Nun erstellt man drei neue Probleme, die man wiederum versucht, mithilfe der Langrange-Relaxierung zu lösen. Dafür werden nach einem bestimmten Schema Kanten für die nächste Lösung entweder "erzwungen" oder "verboten". Alle weiteren Kanten sind "frei". Diese drei Probleme werden gemäß folgender Regeln erstellt, wobei zwei der anliegenden Kanten mit e bzw. f bezeichnet sind:
    • e und f werden zu erzwungenen Kanten, alle anderen werden verboten.
    • e wird erzwungen und f verboten. Alle Kanten, die vorher frei waren, bleiben frei.
    • e wird verboten. Alle andere Kanten bleiben frei, wenn sie es vorher waren.
    Dabei ist wichtig zu wissen, dass diese Regeln sich gegenseitig ausschließen. Eine mithilfe der ersten, zweiten oder dritten Regel erzielte Lösung kann nicht auch durch eine der beiden anderen Regeln entstanden sein.
    Auch die aktuelle Lösung kommt für zukünftige Läufe des Verfahrens nicht mehr in Betracht. Da wir einen Knoten gewählt haben, der an drei Kanten anliegt und die erste Regel genau zwei Kanten an diesem Knoten erzwingt, ändert sich die Anzahl der dort anliegenden Kanten zwangsläufig. Da die beiden anderen Regeln jeweils eine der bisher anliegenden Kanten ausschließen, kann diese Lösung also tatsächlich nicht erneut erreicht werden.
    Ihr Browser unterstützt kein HTML5 Canvas. Bitte verwenden Sie einen modernen Browser, z.B.Mozilla Firefox

    Entstehung des Traveling Salesman Problems

    Das Traveling Salesman Problem oder Problem des Handlungsreisenden, wie es auf deutsch heißt, beschäftigt sich mit der Frage, wie eine Rundtour durch eine gegebene Menge Städte geplant werden muss (ohne eine Stadt doppelt zu besuchen), damit der insgesamt zurückgelegte Weg möglichst kurz ist.
    Dieses Problem taucht in der Literatur zum ersten Mal im Jahr 1831 in einem Buch von Voigt auf. Es trägt den Titel "Der Handlungsreisende wie er sein soll und was er zu thun hat, um Aufträge zu erhalten und eines glücklichen Erfolgs in seinen Geschäften gewiss zu sein. Von einem alten Voyageur." Entscheidend ist darin ein Ausschnitt auf den letzten Seiten:
    [...] Durch geeignete Auswahl und Planung der Tour kann man oft so viel Zeit sparen, daß wir einige Vorschläge zu machen haben. [...] Der wichtigste Aspekt ist, so viele Orte wie möglich zu erreichen, ohne einen Ort zweimal zu besuchen. [...]
    Obgleich diese beiden Sätze die Fragestellung des Traveling Salesman Problems inhaltlich sehr gut treffen, wird der Einzug des Problems in die Mathematik auf einen Beitrag Karl Mengers im Rahmen des Mathematischen Kolloquiums in Wien 1930 zurückgeführt:
    Wir bezeichnen als Botenproblem (weil diese Frage in der Praxis von jedem Postboten, übrigens auch von vielen Reisenden zu lösen ist) die Aufgabe, für endlich viele Punkte, deren paarweise Abstände bekannt sind, den kürzesten die Punkte verbindenden Weg zu finden.
    Natürlich stimmt auch diese Formulierung nicht exakt mit dem Problem des Handlungsreisenden überein, da hier nur nach dem kürzesten Weg, nicht aber nach der kürzesten Rundtour gefragt ist.
    Trotzdem gelangte es von Wien aus 1931/1932 zu Hassler Whitney, der es unter dem heutigen Namen 1934 an der Universität Princeton vorstellte.

    Die Applikation

    Die Applikation stellt einige Algorithmen zur Lösung des Traveling-Salesman-Problems dar. Dabei wurden solche ausgewählt, deren Berechnungsschritte gut zu veranschaulichen und leicht zu beschreiben sind. Die Entwicklung dieser Verfahren liegt aber schon einige Zeit zurück, sodass sie natürlich nicht den aktuellen Stand der Forschung darstellen.

    Mathestudium an der TUM

    Weitere Graphalgorithmen werden auf der Webseite des Lehrstuhls M9 der TU München erklärt.
    Ein Mathematikstudium an der TU München beantwortet alle weiteren Fragen zur Graphentheorie (sofern eine Lösung bekannt ist).

    Ein letzter Hinweis zum Ziel dieser Seite und zu Zitationen

    Der Lehrstuhl M9 der TU München beschäftigt sich mit diskreter Mathematik, angewandter Geometrie und der Optimierung von mathematischen Problemen. Das hier dargestellte Problem und die zugehörigen Algorithmen ist ein bekanntes Beispiel für die Anwendung von Mathematik auf angewandte Probleme (und ist dem Bereich der kombinatorischen Optimierung zuzuordnen). Diese Seite soll dem Leser dabei helfen, die Anwendung von Mathematik auf lebensnahe Problem zu erkennen und einfache mathematische Lösungsverfahren zu verstehen. Die dargestellten Algorithmen wurden deshalb nach Kriterien der Verständlichkeit und Erklärbarkeit ausgewählt, sie stellen keinesfalls den Forschungsgegenstand des Lehrstuhl dar.

    Um diese Seite zu zitieren, nutze bitte die folgenden Angaben:

    Es ist keine Lösung verfügbar.

    Die Berechnung der Lösung läuft zur Zeit noch. Bitte probiere es in ein paar Sekunden noch einmal!

    Die Berechnung der Lösung wurde abgebrochen. Bitte kehre zum Spiel erstellen-Tab zurück und starte ein neues Spiel.