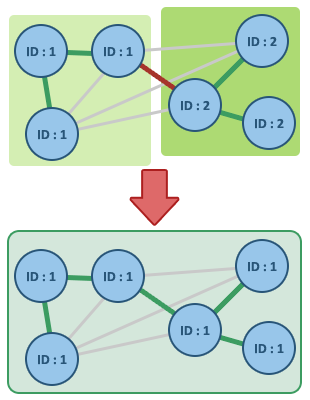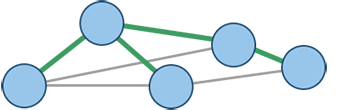
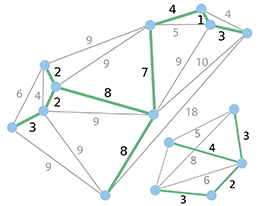
Minimum spanning forest (MSF) shown in green!

What do you want to do first?

Input: Weighted, undirected graph G = (V, E) with weight function l.
Output: A list T of edges representing the MST (or MSF if G is not connected).

BEGIN
  T ← ∅
  queue ← sort {u, v} edges of E using l.
  FOREACH v in G.V
    make-tree(v);
  WHILE queue ≠ ∅ AND trees-count > 1 DO
    {u, v} ← queue.extractMin()
    IF !(T ∪ {{u, v}} has cycle)
      T.add({u, v})
      merge(tree-of(u), tree-of(v))	
END

Speed of the algorithms

The Speed of an algorithm is the total number of individual steps which are performed during the execution. These steps are for example:

• Assignments – Set distance of a node to 20.
• Comparisons – Is 20 greater than 23?
• Comparison and assignment – If 20 is greater than 15, set variable n to 20
• Simple Arithmetic Operations – What is 5 + 5?

Since it can be very difficult to count all individual steps, it is desirable to only count the approximate magnitude of the number of steps. This is also called the running time of an algorithm. Particularly, it is intersting to know the running time of an algorithm based on the size of the input (in this case the number of the vertices and the edges of the graph).

Running time of Kruskal's algorithm

First, sorting the edges using comparison sorts, or adding them to a priority queue can be done proportional to m · log(m) steps (this allows to perform the extractMin() operation in constant time). As m ≤ n * n this time is at most m · log(n^2) = 2 * m · log(n)

Next, a disjoint-set data structure (Union&Find) is used to keep track of which vertices are in which tree. Even a simple disjoint-set data structure can perform operations proportional to log(size).

In each iteration, two find-set() operation and possibly one union() operation are performed. Considering all the edges, the total time required for processing the loop will be a multiply of m · log(n). Adding this value to the time required for sorting the edges, the total time needed for running the algorithm is proportional to m · log(n).

Provided that edges are already sorted or can be sorted in linear time (i.e using counting sort or radix sort), the algorithm can use more sophisticated disjoint-set data structure to run proportional to m · α(n), where α is the extremely slowly growing inverse of the single-valued Ackermann function.

The proof consists of two parts. First, it is proved that the algorithm produces a spanning tree. Second, it is proved that the constructed spanning tree is of minimal weight.

Spanning tree

Let G=(V, E) be a connected, weighted graph and let T be the subgraph of G produced by the algorithm. T cannot have a cycle because the algorithm only chooses those edges which are connecting two different trees. T cannot be disconnected, since the first encountered edge that joins two components of T would have been added by the algorithm. Thus, T is a spanning tree of G.

Minimality

We show that the following proposition P is true by induction: If E1 is the set of edges chosen at any stage of the algorithm, then there is some minimum spanning tree that contains E1.

• Clearly P is true at the beginning, when E1 is empty: any minimum spanning tree will do, and there exists one because a weighted connected graph always has a minimum spanning tree.

  

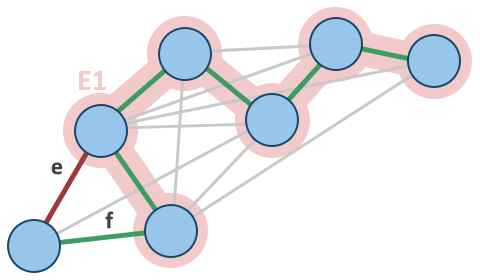
• Now assume P is true for some non-final edge set E1 and let T1 be a minimum spanning tree that contains E1. If the next chosen edge e is also in T1, then P is true for the union of E1 and e. Otherwise, this union T1 + {e} has a cycle C and there is another edge f that is in C but not E1. (If there were no such edge f, then e could not have been added to E1, since doing so would have created the cycle C.) Then T1 − f + e is a tree, and it has the same weight as T1, since T1 has minimum weight and the weight of f cannot be less than the weight of e, otherwise the algorithm would have chosen f instead of e. So T1 − f + e is a minimum spanning tree containing E1 + e and again P holds.
• Therefore, by the principle of induction, P holds when E1 has become a spanning tree, which is only possible if E1 is a minimum spanning tree itself.

Other graph algorithms are explained on the Website of Chair M9 of the TU München.

Furthermore there is an interesting book about shortest paths: Das Geheimnis des kürzesten Weges

Studying mathematics at the TU München answers all questions about graph theory (if an answer is known).

Chair M9 of Technische Universität München does research in the fields of discrete mathematics, applied geometry and the mathematical optimization of applied problems. The algorithms presented on the pages at hand are very basic examples for methods of discrete mathematics (the daily research conducted at the chair reaches far beyond that point). These pages shall provide pupils and students with the possibility to (better) understand and fully comprehend the algorithms, which are often of importance in daily life. Therefore, the presentation concentrates on the algorithms' ideas, and often explains them with just minimal or no mathematical notation at all.

Please be advised that the pages presented here have been created within the scope of student theses, supervised by Chair M9. The code and corresponding presentation could only be tested selectively, which is why we cannot guarantee the complete correctness of the pages and the implemented algorithms.

Naturally, we are looking forward to your feedback concerning the page as well as possible inaccuracies or errors. Please use the suggestions link also found in the footer.

To cite this page, please use the following information:

• Title: Kruskal's Algorithm
• Authors: Wolfgang F. Riedl, Reza Sefidgar; Technische Universität München
• Link: https://www-m9.ma.tum.de/graph-algorithms/mst-kruskal