

- Einführung
- Graph erstellen
- Algorithmus ausführen
- Beschreibung des Algorithmus
- Forschungsaufgabe
- Weiteres
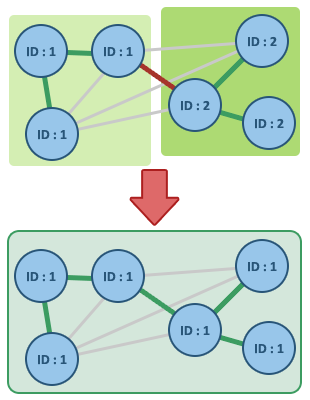
Minimaler aufspannender Wald (MSF) in grün!
Der Minimaler Spannbaum-Algorithmus
Eine Telekommunikationsfirma möchte alle Häuser einer neuen Nachbarschaft ans Internet anbinden. Die einfachste Möglichkeit zur Installation der Kabelverbindungen ist, sie entlang von Straßen zu vergraben. Deshalb beschließt die Firma, die Anschlüsse an Straßenkreuzungen zu nutzen. Wie können die Kosten hierfür minimiert werden, wenn der Preis für die Verbindung von zwei Anschlüssen der Länge des sie verbindenden Kabels entspricht?
Wenn man die Straßen als einen Graphen betrachtet, ist das obige Beispiel eine Instanz des Minimalen Spannbaum Problems. Die Algorithmen von Prim and Kruskal sind zwei bekannte Verfahrten, welche eine alle Knoten verbindende Teilmenge von Kanten minimalen Gewichts eines gewichteten ungerichteten Graphen berechnen können.
Diese Seite präsentiert den Algorithmus von Kruskal, welcher den minimalen Spannbaum (MST) eines zusammenhängenden gewichteten Graphen berechnet. Falls der Graph nicht zusammenhängend ist, so wird der Algorithmus einen minimalen aufspannenden Wald (MSF) finden. Zum Vergleich findest du hier auch ein Einführung zum Algorithmus von Prim.
Was möchtest du zuerst tun?
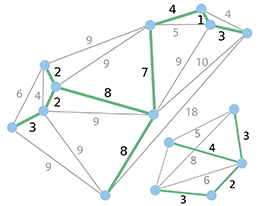
Auf welchem Graph soll der Algorithmus ausgeführt werden?
Nimm ein fertiges Beispiel!
Ändere den Graphen nach deinen Vorstellungen:
- Um einen Knoten zu erstellen, mache einen Doppelklick in das Zeichenfeld.
- Um eine Kante zu erstellen, klicke zunächst auf den Ausgangsknoten und dann auf den Zielknoten.
- Das Kantengewicht kann mit einem Doppelklick auf die Kante verändert werden.
- Ein Rechtsklick löscht Kanten und Knoten.
Lade den veränderten Graphen herunter:
DownloadLade einen existierenden Graphen hoch:
Was nun?
Status des Algorithmus
BEGIN
T ← ∅
queue ← sort {u, v} edges of E using l.
FOREACH v in G.V
make-tree(v);
WHILE queue ≠ ∅ AND trees-count > 1 DO
{u, v} ← queue.extractMin()
IF !(T ∪ {{u, v}} has cycle)
T.add({u, v})
merge(tree-of(u), tree-of(v))
END
Beim Wechsel des Tabs wird der Algorithmus abgebrochen.
Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.
Überprüfe dein Wissen: Wie würde der Algorithmus entscheiden?
BEGIN
T ← ∅
queue ← sort {u, v} edges of E using l.
FOREACH v in G.V
make-tree(v);
WHILE queue ≠ ∅ AND trees-count > 1 DO
{u, v} ← queue.extractMin()
IF !(T ∪ {{u, v}} has cycle)
T.add({u, v})
merge(tree-of(u), tree-of(v))
END
Beim Wechsel des Tabs wird der Algorithmus abgebrochen.
Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.
Wie sieht der (Pseudo-)Code des Algorithmus aus?
Eingabe: Gewichteter, ungerichteter Graph G = (V, E) mit Gewichtsfunktion l.
Ausgabe: Eine Menge von Kanten T, welche den MST bilden
(oder MSF, falls G nicht zusammenhängend ist).
BEGIN
T ← ∅
queue ← sortiere Kanten E nach l.
FOREACH v in G.V
make-tree(v);
WHILE queue ≠ ∅ AND trees-count > 1 DO
{u, v} ← queue.extractMin()
IF !(T ∪ {{u, v}} enthält Kreis)
T.add({u, v})
merge(tree-of(u), tree-of(v))
END
Wie schnell ist der Algorithmus?
Geschwindigkeit von Algorithmen
Die Geschwindigkeit von Algorithmen wird üblicherweise in der Anzahl an Einzelschritten gemessen, die der Algorithmus bei der Ausführung benötigt.
Einzelschritte sind beispielsweise:
- Zuweisungen – Weise Knoten 1 den Wert 20 zu.
- Vergleiche – Ist 20 größer als 23?
- Vergleich und Zuweisung – Falls 20 größer als 15 ist, setze Variable n auf 20.
- Einfache Arithmetische Operationen – Was ist 5 + 5?
Da es sehr schwierig sein kann, diese Einzelschritte exakt zu zählen, möchte man nur die ungefähre Größenordnung der Anzahl Schritte wissen. Man spricht auch von der Laufzeit des Algorithmus. Meistens ist es besonders interessant, zu wissen, wie die Geschwindigkeit des Algorithmus von der Größe der Eingabe (hier: Anzahl Kanten und Knoten im Graph) abhängt.
Laufzeit des Algorithmus von Kruskal
Die Sortierung der Kanten zu Beginn kann in ungefähr m · log(m) Schritten gemacht werden (so kann die extractMin() Operation später in einer Anweisung gemacht werden). Da m ≤ n * n ist die Zeit maximal m · log(n^2) = 2 * m · log(n)
Weiterhin wird eine "Union-Find" Datenstruktur verwendet, um die Zuordnung der Knoten zu den Bäumen zu speichern. Sogar eine einfache Datenstruktur dieser Art kann Operation in einer Zeit proportional zu log(size) ausführen.
In jeder Iteration werden zwei Operationen ausgeführt, um den zu einem Knoten zugehörigen Baum zu finden ("find-set()" Operation) und maximal zwei Bäume vereinigt (ein "union()" Aufruf). Deshalb ist die Gesamtzeit zur Berücksichtigung aller Kanten in der Schleife ein Vielfaches von m · log(n). Wenn man diesen Wert zur Laufzeit der Sortierung der Kanten addiert, ergibt sich eine Gesamtlaufzeit des Algorithmus von m · log(n).
Falls die Kanten bereits sortiert sind oder in linearer Zeit sortiert werden können (das heißt durch die Benutzung von bespielsweise "radix sort"), kann der Algorithmus eine ausgefeiltere "Union-Find" Datenstruktur nützen und somit eine Laufzeit von m · α(n) erreichen, wobei α die sehr langsam wachsende Inverse der Ackermann-Funktion ist.
Arbeitet der Algorithmus korrekt?
Der Beweis besteht aus zwei Teilen. Zuerst begründen wir, dass der Algorithmus einen Spannbaum zurückgibt. Anschließend erklären wir, warum der konstruierte Spannbaum minimales Gewicht hat.
Spannbaum
Nehme einen zusammenhängenden, gewichteten Graphen G=(V, E) und bezeichne mit T den Subgraphen von G, welcher vom Algorithmus erzeugt wurde. T kann keinen Kreis enthalten, da der Algorithmus nur jene Kanten auswählt, welche zwei verschiedene Bäume verbinden. Weiterhin kann T nicht unzusammenhängend sein, da die erste Kante, welche zwei Komponenten von G (welcher zusammenhängend ist) verbinden würde, vom Algorithmus zu T hinzugefügt worden wäre. Deshalb ist T ein Spannbaum von G.
Minimaler Spannbaum
Wir zeigen, dass die folgende Aussage wahr ist: Falls E1 die Kantenmenge in einem bestimmten Schritt des Algorithmus ist, dann gibt es einen minimalen Spannbaum, welcher E1 enthält.
-
Zu Beginn ist die Aussage natürlich wahr: E1 ist leer, und jeder minimale Spannbaum entgenügt für die Aussage. Es existiert ein minimaler Spannbaum, da ein gewichteter, zusammenhängender Graph immer einen minimalen Spannbaum besitzt.
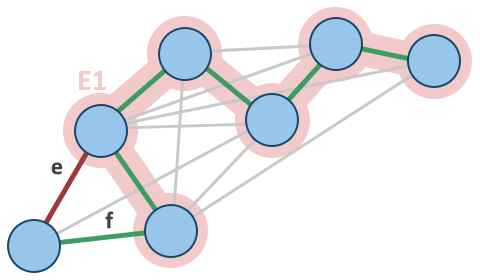
T1 in grün. - Nehmen wir also an, dass der Algorithmus noch nicht fertig ist und die Aussage für eine Kantenmenge E1 wahr ist. Bezeichne mit T1 den minimalen Spannbaum, welcher E1 enthält. Falls die als nächstes ausgewählte Kante e auch in T1 ist, dann ist die Aussage auch für die Vereinigung von E1 und e wahr. Ansonsten enthält diese Vereinigung T1 + {e} einen Kreis C, auf welchem eine weitere Kante f liegt, welche in C aber nicht in E1 ist. (Würde diese Kante nicht existieren, dann hätten wir e nicht zu E1 hinzufügen können, da wir sonst den Kreis C erzeugt hätten.) Dann jedoch ist die Menge T1 − {f} + {e} ein Baum mit dem gleichen Gesamtgewicht wie T1, da erstens T1 minimales Gewicht hat und zweitens das Gewicht von f nicht kleiner sein kann als das von e, sonst hätte der Algorithmus f anstatt von e gewählt. Deshalb ist T1 − {f} + {e} ein minimaler Spannbaum, welcher E1 + {e} enthält. Dementsprechend gilt unsere Aussage wieder.
- Wenn man dies fortführt (das Prinzip nennt sich Beweis durch Induktion), gilt die Aussage auch, wenn E1 ein Spannbaum ist. Dies ist jedoch nur möglich, falls E1 selbst ein minimaler Spannbaum ist.
Wo finde ich noch mehr Informationen zu Graphalgorithmen?
Weitere Graphalgorithmen werden auf der Webseite des Lehrstuhls M9 der TU München erklärt.
Außerdem gibt es ein interessantes Buch zu kürzesten Wegen: Das Geheimnis des kürzesten Weges
Ein Mathematikstudium an der TU München beantwortet alle Fragen zur Graphentheorie (falls eine Lösung bekannt ist).
Ein letzter Hinweis zum Ziel und Inhalt dieser Seite und zu Zitationen
Der Lehrstuhl M9 der TU München beschäftigt sich mit diskreter Mathematik, angewandter Geometrie und der mathematischen Optimierung von angewandten Problemen. Die hier dargestellten Algorithmen sind sehr grundlegende Beispiele für Verfahren der diskreten Mathematik (die tägliche Forschung des Lehrstuhls geht weit darüber hinaus). Die vorliegenden Seiten sollen SchülerInnen und Studierenden dabei helfen, diese auch im realen Leben sehr wichtigen Verfahren (besser) zu verstehen und durch Ausprobieren zu durchdringen. Aus diesem Grund konzentriert sich die Darstellung bewusst auf die Ideen der Algorithmen, und präsentiert diese oftmals unter weitestgehendem Verzicht auf mathematische Notation.
Bitte beachten Sie, dass diese Seiten im Rahmen von studentischen Arbeiten unter Betreuung des Lehrstuhls M9 erstellt wurden. Den dabei entstandenen Code und die zugehörige Darstellung können wir nur punktuell überprüfen, und können deshalb keine Garantie für die vollständige Korrektheit der Seiten und der implementierten Algorithmen übernehmen.
Selbstverständlich freuen wir uns über jegliches (auch kritisches) Feedback bezüglich der Anwendungen sowie eventuellen Ungenauigkeiten und Fehlern der Darstellung und der Algorithmen. Bitte nutzen Sie hierzu den Anregungen-Link, welcher auch rechts in der Fußleiste zu finden ist.
Um diese Seite zu zitieren, nutze bitte die folgenden Angaben:
- Titel: Der Algorithmus von Kruskal
- Autoren: Wolfgang F. Riedl, Reza Sefidgar; Technische Universität München
- Link: https://www-m9.ma.tum.de/graph-algorithms/mst-kruskal