Einführung
Graph erstellen
Algorithmus ausführen
Beschreibung des Algorithmus
Forschungsaufgabe 1
Forschungsaufgabe 2
Weiteres

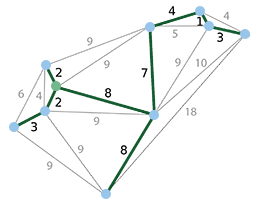
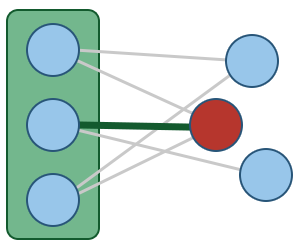
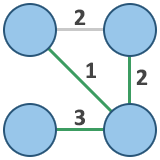
Minimaler Spannbaum (MST) in grün!

Der Minimale Spannbaum-Algorithmus

Eine Telekommunikationsfirma möchte alle Häuser einer neuen Nachbarschaft ans Internet anbinden. Die einfachste Möglichkeit zur Installation der Kabelverbindungen ist, sie entlang von Straßen zu vergraben. Deshalb beschließt die Firma, die Anschlüsse an Straßenkreuzungen zu nutzen. Wie können die Kosten hierfür minimiert werden, wenn der Preis für die Verbindung von zwei Anschlüssen der Länge des sie verbindenden Kabels entspricht?

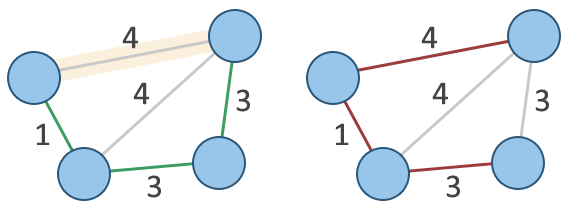
Wenn man die Straßen als einen Graphen betrachtet, ist das obige Beispiel eine Instanz des Minimalen Spannbaum Problems. Die Algorithmen von Prim and Kruskal sind zwei bekannte Verfahren, welche eine alle Knoten verbindende Teilmenge von Kanten minimalen Gewichts eines gewichteten ungerichteten Graphen berechnen können.

Diese Seite präsentiert den Algorithmus von Prim, welcher den minimalen Spannbaum (MST) eines gewichteten zusammenhängenden Graphen berechnet. Zum Vergleich findest du hier auch ein Einführung zum Algorithmus von Kruskal.

Was möchtest du zuerst tun?

SVG Download

Legende

	Knoten
	Kante mit Gewicht 50

Legende

Auf welchem Graph soll der Algorithmus ausgeführt werden?

Nimm ein fertiges Beispiel!

Ändere den Graphen nach deinen Vorstellungen:

Um einen Knoten zu erstellen, mache einen Doppelklick in das Zeichenfeld.
Um eine Kante zu erstellen, klicke zunächst auf den Ausgangsknoten und dann auf den Zielknoten.
Das Kantengewicht kann mit einem Doppelklick auf die Kante verändert werden.
Ein Rechtsklick löscht Kanten und Knoten.

Lade den veränderten Graphen herunter:

Download

Lade einen existierenden Graphen hoch:

Ein

trat auf beim Lesen der Datei:

Fehlerbeschreibung:

Was nun?

SVG Download

Legende

	Wurzel, ein beliebiger Knoten welcher als Wurzel des MST genutzt wird
	Gerade bearbeiteter Knoten
	Knoten in der Warteschlange
	Kante im minimalen Spannbaum

Legende

Status des Algorithmus

rewind Vorspulen

Erklärung
Pseudocode

BEGIN

T ← ∅

FOR i ← 1, ..., n DO

d(v[i]) ← ∞, parent(v[i]) ← NULL

d(v[1]) ← 0, parent(v[1]) ← v[1]

WHILE queue ≠ ∅ DO

u ← queue.extractMin()

IF parent(u) ≠ u

T.add({parent(u), u})

FOR ALL {u, w} ∈ E do

IF w ∈ queue AND l(u, w) < d(w) THEN

d(w) ← l(u, w), parent(w) ← u

ELSE IF parent(w) = NULL THEN

d(w) ← l(u, w), parent(w) ← u

queue.insert(w)

END

Warteschlange:

Beim Wechsel des Tabs wird der Algorithmus abgebrochen.

Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.

Was ist die billigste Kantenmenge, die alle Knoten verbindet?

Minimale Spannbäume

Für einen gegebenen zusammenhängenden, ungerichteten Graphen ist ein Spannbaum ein kreisfreier Subgraph, der alle Knoten verbindet. Offensichtlich kann es in einem Graphen viele Spannbäume geben. Wenn man den Kanten noch Gewichte hinzufügt, dann ist das Gesamtgewicht eines Subgraphen die Summe der einzelnen Kantengewichte. Der Spannbaum mit dem geringsten Gewicht wird minimaler Spannbaum (MST) genannt. Noch allgemeiner formuliert hat jeder ungerichtete Graph einen minimalen Spannwald (MSF), das heißt eine Menge von minimalen Spannbäumen (für jede zusammenhängende Komponente einer).

Der Algorithmus von Prim ist ein "Greedy"-Algorithmus (ein Verfahren, das in jedem Schritt lokal die gierigste/beste Wahl trifft in der Hoffnung, so die globale Lösung zu finden), welches effizient die minimalen Spannbaum eines zusammenhängenden, gewichteten ungerichteten Graphen berechnet. Der Algorithmus könnte zwar auch so modifizert werden, dass er einen minimalen Spannwald für nicht zusammenhängende Graphen findet; allerdings werden hierfür andere Verfahren wie beispielsweise der Algorithmus von Kruskal empfohlen.

Idee des Algorithmus

Kante vor Update — Knoten werden über billigste Kante, welche sie mit einem Knoten im Baum verbindet, zu diesem hinzugefügt.

Der Algorithmus beginnt den Baum mit einem beliebigen einzelnen Knoten, und fügt dann in jeder Iteration eine Kante hinzu. Dies hinzugefügte Kante hat unter allen Kanten, welche den Baum mit Knoten außerhalb des Baums verbinden, minimales Gewicht. Dieser Vorgang wird so lange wiederholt, bis alle Knoten im Baum sind.

Die effizienteste Implementierung des Algorithmus erfolgt über eine Warteschlange. Diese Warteschlange speichert alle Knoten, welche schon besucht wurden, aber noch nicht in den Baum eingefügt sind. Die Reihenfolge der Knoten in der Warteschlange wird über die Distanz jedes Knoten zum Baum bestimmt. In jeder Iteration wird also der Knoten, welcher über die billigste Kante mit dem Baum verbunden ist, aus der Warteschlange entfernt.

Die schrittweise Beschreibung des Algorithmus hat folgende Form. Zuerst werden alle Werte initialisiert:

Ein beliebiger Knoten wird als Wurzel des Baums ausgewählt.
Eine Distanztabelle speichert die Distanzen aller Knoten zum Baum. Die Wurzel hat Distanz Null, und da alle anderen Knoten keine Verbindung zum Baum haben, wird ihre Distanz auf Unendlich gesetzt.
Die Wurzel wird zur Warteschlange hinzugefügt.

Als nächstes behandelt der Algorithmus alle Elemente der Warteschlange. In jeder Iteration wird der erste Knoten der Warteschlange (mit der minimalen Distanz) aus der Schlange entfernt. Zu Beginn ist das die Wurzel, später andere Knoten. Danach werden alle Nachbarn des entfernten Knoten mit ihren sie zum entfernten Knoten verbindenden Kanten betrachtet. Für jeden dieser Knoten wird überprüft, ob das Gewicht dieser verbindenden Kante geringer ist als der aktuelle Distanzwert. Falls das der Fall ist, wird der Distanzwert dieses Nachbarn auf den neuen, geringeren Wert gesetzt. Ansonsten wird der Knoten noch in die Warteschlange eingefügt, falls er das noch nicht ist. Somit werden die ihn verlassenden Kanten später noch betrachtet werden.

Diese Schritte werden so lange wiederholt, bis keine Knoten mehr in der Warteschlange enthalten sind. Dann ist der Algorithmus fertig und gibt als Ergebnis alle Kanten des minimalen Spannbaums zurück.

Konstruktion des MST

Bei jedem Update der Distanztabelle speichert der Algorithmus die Kante, über die die Distanz des Knoten aktualisiert wurde.Die Menge all dieser Kanten ergibt den gesuchten minimalen Spannbaum.

Was nun?

Einen Graph erstellen und den Algorithmus durchspielen

Sein Wissen an den Forschungsaufgaben testen

SVG Download

Legende

	Wurzel, ein beliebiger Knoten welcher als Wurzel des MST genutzt wird
	Aus der Warteschlange entfernter Knoten

Legende

In welcher Reihenfolge werden die Knoten aus der Warteschlange entnommen?

Deine Aufgabe ist es, in der Reihenfolge, in welcher die Knoten aus der Warteschlange entfernt werden, auf die Knoten zu klicken.
Dies entspricht der Reihenfolge, in welcher die Knoten während der Ausführung des Algorithmus rot markiert werden.

Bei Wechsel des Tabs wird die Aufgabe beendet.

Du kannst ein weiteres Browserfenster öffnen, um gleichzeitig die Beschreibung zu lesen.

SVG Download

Legende

	Wurzel, ein beliebiger Knoten welcher als Wurzel des MST genutzt wird
	Gerade bearbeiteter Knoten
	Knoten in der Warteschlange
	Kante im minimalen Spannbaum

Legende

Überprüfe dein Wissen: Wie würde der Algorithmus entscheiden?

rewind Zur nächsten Frage vorspulen

Erklärung
Pseudocode

BEGIN

T ← ∅

FOR i ← 1, ..., n DO

d(v[i]) ← ∞, parent(v[i]) ← NULL

d(v[1]) ← 0, parent(v[1]) ← v[1]

WHILE queue ≠ ∅ DO

u ← queue.extractMin()

IF parent(u) ≠ u

T.add({parent(u), u})

FOR ALL {u, w} ∈ E do

IF w ∈ queue AND l(u, w) < d(w) THEN

d(w) ← l(u, w), parent(w) ← u

ELSE IF parent(w) = NULL THEN

d(w) ← l(u, w), parent(w) ← u

queue.insert(w)

END

Beim Wechsel des Tabs wird der Algorithmus abgebrochen.

Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.

Wie sieht der (Pseudo-)Code des Algorithmus aus?

Eingabe: Gewichteter, zusammenhängender, ungerichteter Graph G = (V, E) mit Gewichtsfunktion l.
Ausgabe: Eine Menge von Kanten T, welche den MST bilden.

BEGIN
  T ← ∅
  FOR i ← 1, ..., n DO
    d(v[i]) ← ∞, parent(v[i]) ← NULL
  d(v[1]) ← 0, , parent(v[1]) ← v[1]
  WHILE queue ≠ ∅ DO
    u ← queue.extractMin()
    IF parent(u) ≠ u
      T.add({parent(u), u})	
    FOR ALL {u, w} ∈ E DO
      IF w ∈ queue AND l(u, w) < d(w) THEN
        d(w) ← l(u, w), parent(w) ← u
      ELSE IF parent(w) = NULL THEN
        d(w) ← l(u, w), parent(w) ← u
        queue.insert(w)
END

Wie schnell ist der Algorithmus?

Geschwindigkeit von Algorithmen

Die Geschwindigkeit von Algorithmen wird üblicherweise in der Anzahl an Einzelschritten gemessen, die der Algorithmus bei der Ausführung benötigt.

Einzelschritte sind beispielsweise:

Zuweisungen – Weise Knoten 1 den Wert 20 zu.
Vergleiche – Ist 20 größer als 23?
Vergleich und Zuweisung – Falls 20 größer als 15 ist, setze Variable n auf 20.
Einfache Arithmetische Operationen – Was ist 5 + 5?

Da es sehr schwierig sein kann, diese Einzelschritte exakt zu zählen, möchte man nur die ungefähre Größenordnung der Anzahl Schritte wissen. Man spricht auch von der Laufzeit des Algorithmus. Meistens ist es besonders interessant, zu wissen, wie die Geschwindigkeit des Algorithmus von der Größe der Eingabe (hier: Anzahl Kanten und Knoten im Graph) abhängt.

Laufzeit des Algorithmus von Prim

Wir nehmen an, dass wir den MST eines Graphen mit n Knoten und m Kanten berechnen wollen.

Da jeder einzelne Knoten betrachtet wird, benötigen wir mindestens n Iterationen.

In jeder Iteration wird der Knoten an erster Position der Warteschlange entfernt und alle seine Nachbarn betrachtet. Das Update der Distanzwerte der Nachbarn und die Auswahl des Knoten mit der kleinsten Distanz benötigt n Schritte. Falls die Warteschlange also als einfache Liste implementiert ist, benötigt der Algorithmus n · n Schritte.

Es ist möglich, die Laufzeit des Algorithmus zu verbessern, indem die Implementierung der Warteschlange verbessert wird. Falls man einen Fibonnaci Heap nutzt, so kann man die Laufzeit des Algorithmus auf m + n · log(n) reduzieren.

Arbeitet der Algorithmus korrekt?

Betrachte einen zusammenhängenden, gewichteten Graphen G=(V, E). In jeder Iteration des Algorithmus von Prim wird eine Kante gesucht, die einen Knoten außerhalb des (noch unvollständigen) Spannbaums mit dem Baum verbindet. Da G zusammenhängend ist, ist dies immer möglich. Das Ergebnis T des Algorithmus ist ein Baum, da die zu T hinzugefügten Knoten alle zusammenhängend sind.

Betrachte einen minimalen Spannbaum T1 des Graphen G. Falls T1=T, dass ist T ein minimaler Spannbaum. Nenne sonst die erste Kante, die während der Konstruktion zu T hinzugefügt wurde und nicht in T1 war, e und bezeichne mit P die Menge der Knoten in T, bevor e hinzugefügt wurde. Dann befindet sich ein Endpunkt von e in P, der andere nicht. Da T1 ein Spannbaum des Graphen G ist, gibt es im Baum T1 einen Pfad, der die beiden Endpunkte verbindet. Wenn man an diesem Pfad entlang geht, findet man mindestens eine Kante mit einem Endpunkt in P und einem außerhalb davon. In der Iteration, in welcher e zum Baum T hinzugefügt wird, hätte man auch Kante f hinzufügen können und das wäre getan worden, wenn ihr Gewicht kleiner als das von Kante e gewesen wäre. Da wir wissen, dass f nicht hinzugefügt wurde, können wir sagen ,dass

w(f) ≥ w(e)

Nenne nun T2 den Baum, welchen wir erhalten, wenn wir Kante f aus T1 entfernen und Kante e hinzufügen. T2 ist immer noch zusammenhängend, hat die selbe Kantenzahl wie T1, und sein summiertes Kantengewicht ist nicht größer als das von T1. Deshalb ist T2 auch ein minimaler Spannbaum von G; zusätzlich enthält er auch Kante e und alle vorher zu T hinzugefügten Kanten. Wenn wir diese Schritte wiederholen, erhalten wir irgendwann einen minimalen Spannbaum des Graphen G, welcher identisch mit T ist. Deshalb ist T ein minimaler Spannbaum.

Der Algorithmus ist dem Dijkstra-Algorithmus sehr ähnlich! Was ist der Unterschied zwischen den beiden?

Beim Vergleich beider Algorithmen fällt auf, dass beide eine Warteschlange nutzen, um unbesuchte Knoten mit einem zugehörigen Distanzwert d zu speichern. In jeder Iteration wird dann das minimale Element der Warteschlange entfernt und der Distanzwert entsprechend verändert. (Eine genaue Erklärung des Dijkstra-Algorithmus findest du in diesem Tutorial.)

Der Dijkstra-Algorithmus konstruiert ausgehend von einer Wurzel einen Baum, welcher die kürzesten Wege von dieser Wurzel anzeigt. Dieser Baum hat genau die Eigenschaft, dass der Pfad von der Wurzel zu jedem Knoten den kürzesten Weg angibt (siehe nächste Graphik). Der Algorithmus von Prim hingegen erzeugt einen minimalen Spannbaum des Graphen, das heißt einen Baum welcher alle Knonten verbindet und dessen Gesamtgewicht minimal ist. Die Länge eines Pfades zwischen einem Knoten und der Wurzel in diesem Baum muss nicht der kürzeste Pfad im gesamten Graphen sein.

Das unterschiedliche Verhalten des Dijkstra-Algorithmus erklärt sich dadurch, dass die Distanzmatrix mit der Summe der neuen Kanteund des Entfernung des Vorgängerknotens von der Wurzel aktualisiert wird. Beim Algorithmus von Prim hingegen wird nur das Gewicht der neuen Kante genutzt (welches der Distanz des Zielknotens vom Baum entspricht), um die Distanzmatrix zu aktualisieren.

Dijkstra-Algorithmus:
// Initialisierung ...
WHILE queue ≠ ∅ DO
    // Entfernen des minimalen Elements aus Warteschlange ...
    FOR ALL {u, w} ∈ E DO
        dist ← d(u) + l(u, w)
        IF w ∈ queue AND dist < d(w) THEN
            d(w) ← dist
        // Rest des Algorithmus ...

Algorithmus von Prim:
// Initialisierung ...
WHILE queue ≠ ∅ DO
    // Entfernen des minimalen Elements aus Warteschlange ...
    FOR ALL {u, w} ∈ E DO
        IF w ∈ queue AND l(u, w) < d(w) THEN
            d(w) ← l(u, w)
        // Rest des Algorithmus...

Wo finde ich noch mehr Informationen zu Graphalgorithmen?

Weitere Graphalgorithmen werden auf der Webseite des Lehrstuhls M9 der TU München erklärt.

Außerdem gibt es ein interessantes Buch zu kürzesten Wegen: Das Geheimnis des kürzesten Weges

Ein Mathematikstudium an der TU München beantwortet alle Fragen zur Graphentheorie (falls eine Lösung bekannt ist).

Ein letzter Hinweis zum Ziel und Inhalt dieser Seite und zu Zitationen

Der Lehrstuhl M9 der TU München beschäftigt sich mit diskreter Mathematik, angewandter Geometrie und der mathematischen Optimierung von angewandten Problemen. Die hier dargestellten Algorithmen sind sehr grundlegende Beispiele für Verfahren der diskreten Mathematik (die tägliche Forschung des Lehrstuhls geht weit darüber hinaus). Die vorliegenden Seiten sollen SchülerInnen und Studierenden dabei helfen, diese auch im realen Leben sehr wichtigen Verfahren (besser) zu verstehen und durch Ausprobieren zu durchdringen. Aus diesem Grund konzentriert sich die Darstellung bewusst auf die Ideen der Algorithmen, und präsentiert diese oftmals unter weitestgehendem Verzicht auf mathematische Notation.

Bitte beachten Sie, dass diese Seiten im Rahmen von studentischen Arbeiten unter Betreuung des Lehrstuhls M9 erstellt wurden. Den dabei entstandenen Code und die zugehörige Darstellung können wir nur punktuell überprüfen, und können deshalb keine Garantie für die vollständige Korrektheit der Seiten und der implementierten Algorithmen übernehmen.

Selbstverständlich freuen wir uns über jegliches (auch kritisches) Feedback bezüglich der Anwendungen sowie eventuellen Ungenauigkeiten und Fehlern der Darstellung und der Algorithmen. Bitte nutzen Sie hierzu den Anregungen-Link, welcher auch rechts in der Fußleiste zu finden ist.

Um diese Seite zu zitieren, nutze bitte die folgenden Angaben:

Titel: Der Algorithmus von Prim
Autoren: Wolfgang F. Riedl, Reza Sefidgar; Technische Universität München
Link: https://www-m9.ma.tum.de/graph-algorithms/mst-prim