Visualizations of Graph Algorithms
Graphs are a widely used model to describe structural relations.
They are built of nodes, which are connected by edges (both directed or undirected).
Some prominent examples for the application of graphs are:
-
Routing: In this case nodes represent important places (junctions, cities), while edges correspond to roads connecting these places. A one-way road is represented by a directed edge.
-
Communication networks: Here, nodes are phones, modems, server, ISPs and more, edges are data lines connecting them.
-
Gantt diagrams for sequence planning: Nodes correspond to phases of the projects, directed edges to dependencies between sections.
-
Representation of hierarchical structures: Nodes could correspond to people or departments and edges visualize a hierarchy of command.
Handling such models is an important area of mathematics and computer science. Some important algorithms of this area are presented and explained in the following, including both an interactive applet and pseudocode.
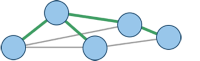
Minimum Spanning Trees
A spanning tree is a set of edges that connect all nodes of a graph but does not have any superfluous edges. The problem of finding a spanning tree (usually of minimum cost) is common in communication networks where it is important that every node can communicate with all other nodes (not necessarily directly). It also occurs in distribution networks (e.g., supply houses of a block with water through a connected network of pipes, electricity networks).
Algorithms: Kruskal's Algorithm, Prim's Algorithm
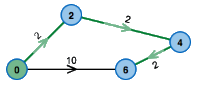
Shortest Paths
One of the most common applications of graphs in everyday life is the representation of infrastructure and communication networks. A street map, bus lines in a city or the flights offered by an airline; they can all be represented by a graph.
The search for a paths between given nodes in these graphs is of great importance. Of special interest are ‘cost efficient’ paths, where ‘cost efficient’ can have diverse interpretations: Maybe it is the shortest or fastest way, the one that can be traversed with minimum fuel consumption, paying a minimum fare or one that avoids speed traps.
Algorithms: Floyd-Warshall Algorithm, Bellman-Ford Algorithm, A* Algorithm, Dijkstra's Algorithm
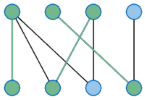
Matching
The Matching Problem deals with the search of a relation between two different sets. A classic example is the so-called ‘Marriage Problem’, in which a set of women and a set of men are given. In addition, we have information on who would accept whom as a potential life partner. A matching then is a set of couples that are ‘compatible’ with one another. The Weighted Matching Problem is a more general case that gives preferences to different relations in order to obtain the best allocation possible. This problem can be solved by the Hungarian Method.
Algorithms: Blossom Algorithm, Hungarian Method, Hopcroft-Karp Algorithm
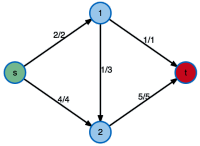
Network Flow
A very common problem in graphs and networks is the computation of flows. Examples include the flow of goods in a logistics system, information in a communication network, or natural gas in a pipeline network. Usually, one is interested either in computing a maximal flow, where the amount of goods to be transported along an edge is bounded by a capacity limit and one wants to route the maximal flow possible from some source node to a given target. Alternatively, one might be interested in routing a given amount of flow in a cost-efficient way, that problem is known as minimum cost flow.
Algorithms: Ford-Fulkerson Algorithm, Cycle-Cancelling Algorithm
Routing
A classical problem in graph theory is the Eulerian Path Problem, which asks for paths or cycles that traverse all edges of a given graph exactly once. The problem was first formulated in the following form: ‘The river Pregel divides the town of Königsberg (Kaliningrad nowadays) into five parts that are connected by seven bridges. Is there a tour that passes each bridge exactly once?’
The aim of the related Chinese Postman Problem is to find a shortest path in a graph, such that this path uses each edge (directed or undirected) at least once and returns to the starting point. The most prominent example for this problem is a postman that delivers mail in some part of town and thus has to walk down every street at least once. In the Traveling Salesperson Problem the objective is to find a minimum length tour through all nodes of a graph, starting and ending at the same point.
Algorithms: Traveling Salesperson Problem, Chinese Postman, Hierholzer's Algorithm