Matching

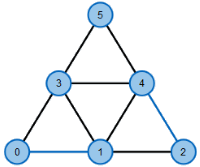
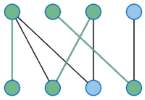
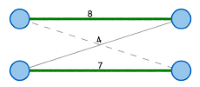
The Matching Problem deals with the search of a relation between two different sets. A classic example is the so-called ‘Marriage Problem’, in which a set of women and a set of men are given. In addition, we have information on who would accept whom as a potential life partner. A matching then is a set of couples that are ‘compatible’ with one another. The Weighted Matching Problem is a more general case that gives preferences to different relations in order to obtain the best allocation possible. This problem can be solved by the Hungarian Method.