Routing

A classical problem in graph theory is the Eulerian Path Problem, which asks for paths or cycles that traverse all edges of a given graph exactly once. The problem was first formulated in the following form: ‘The river Pregel divides the town of Königsberg (Kaliningrad nowadays) into five parts that are connected by seven bridges. Is there a tour that passes each bridge exactly once?’

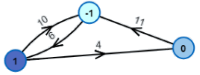
The aim of the related Chinese Postman Problem is to find a shortest path in a graph, such that this path uses each edge (directed or undirected) at least once and returns to the starting point. The most prominent example for this problem is a postman that delivers mail in some part of town and thus has to walk down every street at least once. In the Traveling Salesperson Problem the objective is to find a minimum length tour through all nodes of a graph, starting and ending at the same point.