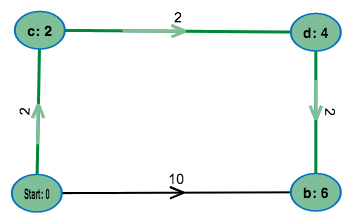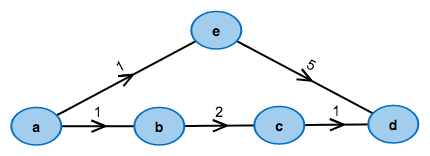
Einführung
Graph erstellen
Algorithmus ausführen
Beschreibung des Algorithmus
Forschungsaufgabe 1
Forschungsaufgabe 2
Forschungsaufgabe 3
Weiteres

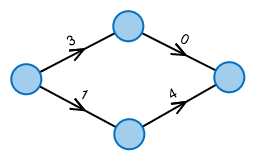
Wie komme ich am günstigsten von links nach rechts?

Der Klassiker unter den Kürzeste-Wege-Algorithmen

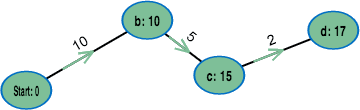
Du würdest gerne wissen, ob du von München aus schneller in Köln bist, wenn du über Stuttgart fährst oder Würzburg fährst? Dann könnte der Dijkstra-Algorithmus hilfreich für dich sein! Mit diesem Algorithmus kannst du unter anderem in einem Graphen, dessen Kanten beispielsweise mit den Distanzen zwischen verschiedenen Städten beschriftet sind, den kürzesten Weg zwischen zwei Städten ermitteln. Aber auch der kürzeste Weg von einer Stadt aus zu allen anderen Städten lässt sich mit dem Dijkstra-Algorithmus leicht bestimmen. Natürlich können die Kantenbeschriftungen auch etwas anderes repräsentieren, wie zum Beispiel die Mautkosten auf den Autobahnen zwischen den Städten.

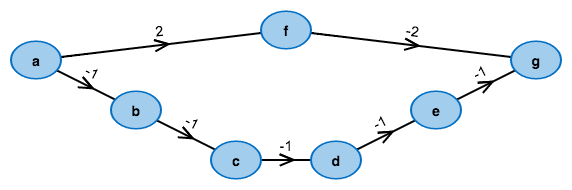
Wichtig beim Dijkstra-Algorithmus ist, dass die Kantenkosten (so nennt man die Kantenbeschriftungen im Allgemeinen) nicht negativ sein dürfen.

Hier wird der Dijkstra-Algorithmus vorgestellt, der günstigste Wege bei nicht-negativen Kosten berechnet.

Was möchtest du zuerst tun?

SVG Download

Legende

	Knoten
	Kante mit Gewicht 50

Legende

Auf welchem Graph soll der Algorithmus ausgeführt werden?

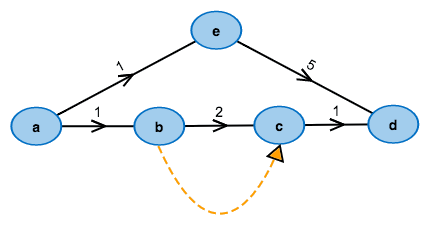
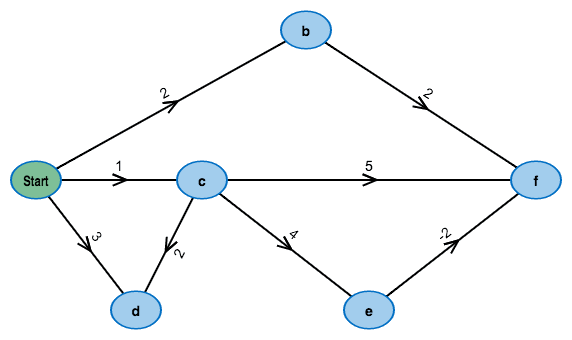
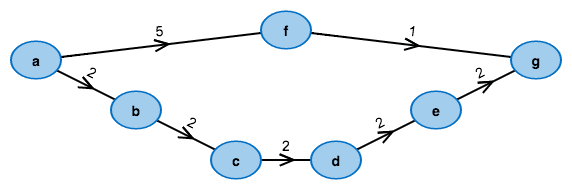
Nimm ein fertiges Beispiel!

Ändere den Graphen nach deinen Vorstellungen:

Um einen Knoten zu erstellen, mache einen Doppelklick in das Zeichenfeld.
Um eine Kante zu erstellen, klicke zunächst auf den Ausgangsknoten und dann auf den Zielknoten.
Das Kantengewicht kann mit einem Doppelklick auf die Kante verändert werden.
Ein Rechtsklick löscht Kanten und Knoten.

Lade den veränderten Graphen herunter:

Download

Lade einen existierenden Graphen hoch:

Ein

trat auf beim Lesen der Datei:

Fehlerbeschreibung:

Was nun?

SVG Download

Legende

	Startknoten, von dem aus die Entfernungen und günstigsten Wege berechnet werden.
	Knoten, der gerade bearbeitet wird
	Knoten, der sich in der Warteschlange befindet
	"Vorgängerkante", die der günstigste Weg zum Knoten benutzt.

Legende

Status des Algorithmus

rewind Vorspulen

Erklärung
Pseudocode

BEGIN

d(v[1]) ← 0

FOR i = 2,..,n DO

d(v[i]) ← ∞, parent(v[i]) ← NULL

WHILE queue ≠ ∅ DO

u = queue.extractMin()

FOR ALL (u,w) ∈ E DO

dist ← d(u) + l(u,w)

IF w ∈ queue AND d(w) > dist DO

d(w) = dist, parent(w) = (u,w)

ELSE IF parent(w) == NULL THEN

d(w) = dist, parent(w) = (u,w)

queue.insert(w,dist)

END

Warteschlange:

Beim Wechsel des Tabs wird der Algorithmus abgebrochen.

Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.

Wie komme ich am günstigsten von links nach rechts?

Kürzeste Wege

Oft möchte man wissen, welches der kürzeste Weg von a nach b ist. Dazu kann man Orte als Knoten in einem Graphen darstellen, welche durch Kanten verbunden sind. Diese Kanten stellen die Wege zwischen den Orten dar. Sie können Beschriftungen haben wie Weglängen in Metern oder Kilometern, aber auch Fahrzeiten oder Mautgebühren für den Weg.

Die Kantenbeschriftungen werden im Allgemeinen als Kantenkosten oder -gewichte bezeichnet.

Mit dem Algorithmus von Dijkstra kann man kürzeste beziehungsweise kostengünstigste Wege berechnen, sofern alle Kosten positive Zahlen sind. Falls auch negative Zahlen auftreten, funktioniert der Algorithmus nicht mehr. In diesem Falle sollte man auf den Bellman-Ford-Algorithmus zurückgreifen, dieser kann auch mit negativen Kantenkosten umgehen.

Idee des Algorithmus

Kante vor Update — Die Kante ist eine Abkürzung:
Wir wissen, dass es uns 20 kostet, um vom Startknoten zum linken Knoten zu gelangen. Der Weg vom linken zum rechten Knoten kostet 1.

Der Dijkstra-Algorithmus berechnet die Kosten der günstigsten Wege von einem Startknoten aus zu allen anderen Knoten im Graph.

Der Algorithmus beginnt bei einem Startknoten und wählt schrittweise über die als nächstes erreichbaren Knoten die momentan günstigsten Wege aus. Dabei kann er auch Verbesserungen vornehmen. Das tut er so lange, bis alle Knoten besucht wurden und kein besserer Weg mehr gefunden wurde.

Um den Algorithmus auszuführen, braucht man eine Warteschlange. Dort werden alle Knoten, die man bereits gefunden hat, eingefügt. Der Knoten, zu dem momentan der güstigste Weg vom Startknoten aus führt, steht ganz vorne in dieser Warteschlange.

Zunächst wird der Algorithmus initialisiert:

Der Weg zum Startknoten hat Kosten 0, denn seine Entfernung zu sich selbst ist natürlich 0.
Zu den anderen Knoten ist noch kein Weg bekannt, darum werden ihre Kosten zunächst mit unendlich bewertet. Im Laufe des Algorithmus sollen diese Kosten verbessert werden, wobei sich der Algorithmus immer den bisher günstigsten gefundenen Weg zu jedem Knoten merkt.
Der Startknoten wird in die Warteschlange eingefügt.

Nun wird der vorderste Knoten aus der Warteschlange entnommen. Zu Beginn kann dies nur der Startknoten sein. Dann werden alle Nachbarknoten des entnommenen Knotens mit den jeweiligen Kanten betrachtet und auf folgende Bedingung geprüft: Ist der Knoten in der Warteschlange enthalten und sind die Kosten über die neue Kante geringer als die bisherigen Kosten?

Falls dies der Fall ist, werden die Kosten für diesen Knoten auf den neuen Wert verringert. Ansonsten wird auf eine weitere Bedingung geprüft: Ist der Knoten bisher noch gar nicht besucht worden? Falls ja, wird er nun in die Warteschlange eingefügt, damit später auch die Kanten, die von ihm aus weggehen, betrachtet werden können. Außerdem erhält dieser Knoten die Kosten, die sich aus der Summe der Kosten zu seinem Vorgängerknoten und den Kosten der neuentdeckten Kante zu ihm selbst ergeben.

Es werden nun so lange Knoten aus der Warteschlange entnommen und ihre Nachbarknoten auf diese beiden Bedingungen geprüft, bis keine Knoten mehr in der Warteschlange enthalten sind. Dann ist der Algorithmus fertig und hat von dem Startknoten ausgehend zu allen anderen Knoten die jeweils günstigsten Wege gefunden.

Graph mit eingezeichneten Abstandswerten — Der grüne Weg vom Startknoten ist der günstigste Weg. Er benutzt 3 Kanten.

Konstruktion des günstigsten Weges

Bei jeder Aktualisierung der Kosten speichert der Algorithmus die Kante, mit deren Hilfe er aktualisiert wurde, als Vorgängerkante des Knotens.

Am Ende des Algorithmus kann dann der günstigste Weg für jeden Knoten konstruiert werden, indem man so lange über Vorgängerkanten läuft, bis man am Startknoten angekommen ist.

Wenn es von dem Startknoten aus zu einem Knoten keinen Weg gibt, so bleiben seine Kosten unendlich, was bedeutet, das dieser Knoten niemals erreichbar ist.

Was nun?

Einen Graph erstellen und den Algorithmus durchspielen

Sein Wissen an den Forschungsaufgaben testen

SVG Download

Legende

	Startknoten, von dem aus die Entfernungen und günstigsten Wege berechnet werden.
	Knoten, der korrekt ausgewählt wurde

Legende

In welcher Reihenfolge werden die Knoten aus der Warteschlange entnommen?

Bei Wechsel des Tabs wird die Aufgabe beendet.

Du kannst ein weiteres Browserfenster öffnen, um gleichzeitig die Beschreibung zu lesen.

SVG Download

Legende

	Startknoten, von dem aus die Entfernungen und günstigsten Wege berechnet werden.
	Kante, für die die richtigen Kosten gewählt wurden
	Kante, für die falsche Kosten eingetragen wurden.

Legende

Welche Kosten haben die Kanten?

Entfernungen der Knoten:

	Start	b	c	d	e	f	g	h	i
Initiali- sierung	0	∞	∞	∞	∞	∞	∞	∞	∞
1. Schritt		3	2	4					34
2. Schritt						14
3. Schritt					12	13
4. Schritt					6		8
5. Schritt						12	7
6. Schritt						8		37
7. Schritt								36
8. Schritt								35
9. Schritt								35

Welche Kosten haben die Kanten?

Hier siehst du in einer Tabelle, welche Entfernungen die Knoten zum Startknoten in welcher Runde haben. Allerdings sind nicht alle Felder ausgefüllt.

Kannst du herausfinden, welche Kosten die Kanten haben? Klicke einfach doppelt auf eine Kante im Zeichenbereich und trage die Kosten ein, die diese Kante haben muss.

Beim Wechsel des Tabs wird die Aufgabe abgebrochen.

Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.

SVG Download

Legende

	Startknoten, von dem aus die Entfernungen und günstigsten Wege berechnet werden.
	Knoten, der gerade bearbeitet wird
	Knoten, der sich in der Warteschlange befindet
	"Vorgängerkante", die der günstigste Weg zum Knoten benutzt.

Legende

Überprüfe dein Wissen: Wie würde der Algorithmus entscheiden?

rewind Zur nächsten Frage vorspulen

Erklärung
Pseudocode

BEGIN

d(v[1]) ← 0

FOR i = 2,..,n DO

d(v[i]) ← ∞, parent(v[i]) ← NULL

WHILE queue ≠ ∅ DO

u = queue.extractMin()

FOR ALL (u,w) ∈ E DO

dist ← d(u) + l(u,w)

IF w ∈ queue AND d(w) > dist DO

d(w) = dist, parent(w) = (u,w)

ELSE IF parent(w) == NULL THEN

d(w) = dist, parent(w) = (u,w)

queue.insert(w,dist)

END

Beim Wechsel des Tabs wird der Algorithmus abgebrochen.

Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.

Wie sieht der (Pseudo-)Code des Algorithmus aus?

Eingabe: Gewichteter, ungerichteter oder gerichteter Graph G=(V,E) mit Gewichtsfunktion l,
         wobei alle Gewichte positiv sind.
Ausgabe: Eine Liste {d(v[j]) : j = 1,..,n}, 
         welche die Distanzen dist(v[1],v[j]) = d(v[j]) enthält.


BEGIN
    d(v[1]) ← 0
    FOR i = 2,..,n DO
        d(v[i]) ← ∞, parent(v[i]) ← NULL
    WHILE queue ≠ ∅ DO
        u = queue.extractMin()
        FOR ALL (u,w) ∈ E DO
            dist ← d(u) + l(u,w)
            IF w ∈ queue AND d(w) > dist DO
                d(w) = dist, parent(w) = (u,w)
            ELSE IF parent(w) == NULL THEN
                d(w) = dist, parent(w) = (u,w)
                queue.insert(w,dist)
END

Wie schnell ist der Algorithmus?

Geschwindigkeit von Algorithmen

Die Geschwindigkeit von Algorithmen wird üblicherweise in der Anzahl an Einzelschritten gemessen, die der Algorithmus bei der Ausführung benötigt.

Einzelschritte sind beispielsweise:

Zuweisungen – Weise Knoten 1 den Wert 20 zu.
Vergleiche – Ist 20 größer als 23?
Vergleich und Zuweisung – Falls 20 größer als 15 ist, setze Variable n auf 20.
Einfache Arithmetische Operationen – Was ist 5 + 5 ?

Da es sehr schwierig sein kann, diese Einzelschritte exakt zu zählen, möchte man nur die ungefähre Größenordnung der Anzahl Schritte wissen. Man spricht auch von der Laufzeit des Algorithmus. Meistens ist es besonders interessant, zu wissen, wie die Geschwindigkeit des Algorithmus von der Größe der Eingabe (hier: Anzahl Kanten und Knoten im Graph) abhängt.

Laufzeit des Dijkstra-Algorithmus

Nehmen wir an, dass der Dijkstra-Algorithmus auf einem Graph mit n Knoten und m Kanten ausgeführt wird.

Da jeder Knoten des Graphen betrachtet wird, brauchen wir mindestens n Schritte.

Um einen Knoten zu behandeln, muss er zuerst aus der Warteschlange entnommen werden. Da wir jedoch immer nur den Knoten, der momentan die geringste Distanz zum Startknoten hat, entnehmen, kann man sich die Warteliste so vorstellen, dass aus allen n Knoten derjenige mit der geringsten Distanz gesucht wird. Um die Knoten auszuwählen braucht der Algorithmus also n · n Einzelschritte.

Um neue Knoten in die Warteschlange einzufügen, werden die Nachbarknoten der ausgehenden Kanten dieses Knotens betrachtet und anhand des Gewichts entschieden, ob der Nachbarknoten in die Warteschlange eingereiht wird oder nicht. Somit werden alle erreichbaren Kanten betrachtet, was bedeutet, dass der Algortihmus weitere m Einzelschritte benötigt.

Insgesamt liegt die Laufzeit des Algortihmus also in der Größenordnung m + n², wenn man die Warteschlange als Liste von Knoten betrachtet.

Es ist auch möglich diese Laufzeit weiter zu verbessern, sodass sie nur noch in der Größenordnung m + n · log(n) liegt. Dazu muss man jedoch für die Warteschlange eine andere Datenstruktur, nämlich einen Heap verwenden.

Berechnet der Algorithmus wirklich die kürzesten Wege?

Ein Beweis durch Widerspruch

Da bei diesem Algorithmus die Kantenkosten positiv sein müssen, gilt folgende Aussage: Alle Teilstrecken, die auf einem kürzesten Weg liegen, sind ebenfalls kürzeste Wege. Um diese Aussage zu beweisen, nehmen wir das Gegenteil an: Es gibt eine Teilstrecke, die auf einem kürzesten Weg liegt, die selbst aber kein kürzester Weg ist. Sei dies in unserem Beispiel die Teilstrecke zwischen b und c, die auf dem kürzesten Weg von a nach d liegt.

Wenn diese Teilstrecke nun kein kürzester Weg ist, dann muss es einen anderen kürzeren Weg geben. Dieser Weg ist durch den orangen Pfeil in dem untenstehenden Bild dargestellt. Nun gibt es einen neuen Weg von a nach d, der zwischen b und c den orangenen Weg benutzt und kürzer sein muss als der alte Weg. Dies widerspricht aber unserer Annahme, dass der ursprüngliche Weg von a nach d bereits ein kürzester Weg war.

Gegenbeispiel — Der orangene Weg sei irgendein kürzerer Weg von b nach c

Da wir einen Widerspruch zu dem Gegenteil unserer Aussage gefunden haben, gilt unsere eigentliche Aussage, dass alle Teilstrecken, die auf einem kürzesten Weg liegen, ebenfalls kürzeste Wege sind. Damit wissen wir auch, dass alle Wege, die der Algorithmus vom Startknoten aus berechnet, kürzeste Wege sind.

Wie löst man das Problem negativer Kantenkosten?

In Forschungsaufgabe 3 hast du gesehen, dass negative Kantenkosten beim Dijkstra-Algorithmus nicht erlaubt sind, da andernfalls nicht garantiert werden kann, dass die richtigen kürzesten Wege gefunden werden: Der Dijkstra-Algorithmus findet vom Startknoten zum Knoten f einen kürzesten Weg mit Kosten 4, obwohl der kürzeste Weg eigentlich Kosten 3 hätte.

Negatives Beispiel aus Forschungsaufgabe 3 — Beispielgraph aus Forschungsaufgabe 3

Was macht man nun also, wenn eine Kante negative Kosten hat? Eine Möglichkeit wäre es, alle Kantenkosten mit einer Zahl zu addieren, die groß genug ist, um alle Kantenkosten positiv werden zu lassen. Man könnte zum Beispiel alle Kantenkosten um den Betrag der günstigsten Kante vergrößern. Möchte man Kanten mit Kosten 0 vermeiden, addiert man diesen Betrag + 1. Im untenstehenden Beispiel hat die günstigste Kante Kosten -2, also würden wir zu allen Kosten 3 dazuaddieren.

Negatives Beispiel — Günstigster Weg von a nach g ist a-b-c-d-e-g

Bevor wir die Kantenkosten positiv gemacht hatten, war der kürzeste Weg von a nach g der Weg a-b-c-d-e-g mit Gesamtkosten -5 gewesen. Nun ist der kürzeste Weg a-f-g mit Gesamtkosten 6. Da wir in erster Linie an dem kürzesten Weg interessiert waren, ist es nicht so schlimm, dass die Gesamtkosten unterschiedlich sind. Es wurde jedoch ein vollkommen anderer Weg als kürzester Weg gefunden. Also hilft es nicht weiter, wenn wir alle Kanten mit einer großen Zahl addieren.

Negatives Beispiel mit positiven Kantenkosten — Günstigster Weg von a nach g ist a-f-g

Um mit negativen Kantenkosten umgehen zu können, müsste auch jeder bereits abgearbeitete Knoten wieder aktualisiert werden können, falls ein noch kürzerer Weg zu ihnen gefunden wurde. Ein Algorithmus, der das kann, ist der Bellman-Ford-Algorithmus

Wo finde ich noch mehr Informationen zu Graphalgorithmen?

Weitere Graphalgorithmen werden auf der Webseite des Lehrstuhls M9 der TU München erklärt.

Außerdem gibt es ein interessantes Buch zu kürzesten Wegen: Das Geheimnis des kürzesten Weges

Ein Mathematikstudium an der TU München beantwortet alle Fragen zur Graphentheorie (falls eine Lösung bekannt ist).

Ein letzter Hinweis zum Ziel und Inhalt dieser Seite und zu Zitationen

Der Lehrstuhl M9 der TU München beschäftigt sich mit diskreter Mathematik, angewandter Geometrie und der mathematischen Optimierung von angewandten Problemen. Die hier dargestellten Algorithmen sind sehr grundlegende Beispiele für Verfahren der diskreten Mathematik (die tägliche Forschung des Lehrstuhls geht weit darüber hinaus). Die vorliegenden Seiten sollen SchülerInnen und Studierenden dabei helfen, diese auch im realen Leben sehr wichtigen Verfahren (besser) zu verstehen und durch Ausprobieren zu durchdringen. Aus diesem Grund konzentriert sich die Darstellung bewusst auf die Ideen der Algorithmen, und präsentiert diese oftmals unter weitestgehendem Verzicht auf mathematische Notation.

Bitte beachten Sie, dass diese Seiten im Rahmen von studentischen Arbeiten unter Betreuung des Lehrstuhls M9 erstellt wurden. Den dabei entstandenen Code und die zugehörige Darstellung können wir nur punktuell überprüfen, und können deshalb keine Garantie für die vollständige Korrektheit der Seiten und der implementierten Algorithmen übernehmen.

Selbstverständlich freuen wir uns über jegliches (auch kritisches) Feedback bezüglich der Anwendungen sowie eventuellen Ungenauigkeiten und Fehlern der Darstellung und der Algorithmen. Bitte nutzen Sie hierzu den Anregungen-Link, welcher auch rechts in der Fußleiste zu finden ist.

Um diese Seite zu zitieren, nutze bitte die folgenden Angaben:

Titel: Der Dijkstra - Algorithmus
Autoren: Melanie Herzog, Wolfgang F. Riedl, Lisa Velden; Technische Universität München
Link: https://www-m9.ma.tum.de/graph-algorithms/spp-dijkstra