

- Einführung
- Graph erstellen
- Algorithmus ausführen
- Beschreibung des Algorithmus
- Forschungsaufgabe 1
- Forschungsaufgabe 2
- Weiteres
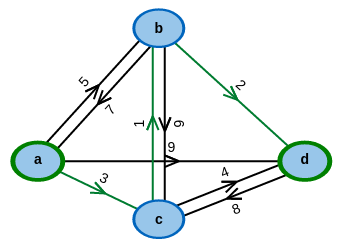
Was sind die günstigsten Wege zwischen Knotenpaaren?
Kürzeste Pfade zwischen allen Paaren von Knoten
Wenn man die Distanzen zwischen verschiedenen Orten berücksichtigt, zum Beispiel im Bereich Logistik, kommen die Aufgaben über die kürzeste Wege oft vor. In diesen Situationen können die Orte als die Knoten und die Kanten als Wege im Graph dargestellt werden.
Bei der Lösung vieler Aufgaben muss man die kürzeste Wege zwischen allen Paaren von Knoten eines Graphen bestimmen und deren Längen berechnen. Der Floyd-Warshall Algorithmus, der dieses Problem löst, kann auf dem beliebigen Graph ausgeführt werden, wobei es wichtig ist, dass er keine negative Kreise enthält. Falls es negative Kreise im Graph gibt, dann können die genutzt werden um beliebig kleinen (negativen) Wege zwischen einigen Knoten zu konstruieren. In diesem Fall kann der Algorithmus keinen optimalen Wert erzeugen.
Hier wird der Floyd-Warshall-Algorithmus vorgestellt, der günstigste Wege zwischen allen Paaren von Knoten berechnet.
Was möchtest du zuerst tun?
Auf welchem Graph soll der Algorithmus ausgeführt werden?
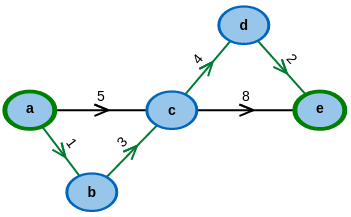
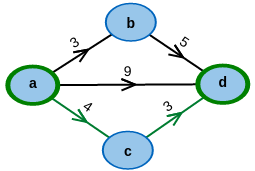
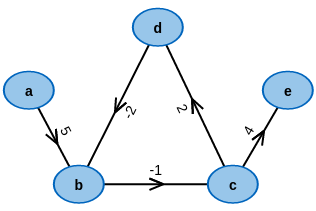
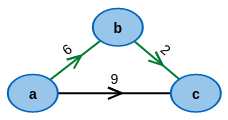
Nimm ein fertiges Beispiel!
Ändere den Graphen nach deinen Vorstellungen:
- Um einen Knoten zu erstellen, mache einen Doppelklick in das Zeichenfeld.
- Um eine Kante zu erstellen, klicke zunächst auf den Ausgangsknoten und dann auf den Zielknoten.
- Das Kantengewicht kann mit einem Doppelklick auf die Kante verändert werden.
- Ein Rechtsklick löscht Kanten und Knoten.
Lade den veränderten Graphen herunter:
DownloadLade einen existierenden Graphen hoch:
Was nun?
Status des Algorithmus
BEGIN
FOR ALL v ∈ V
d[v][v] ← 0
FOR ALL (u,v) ∈ E
d[u][v] ← w(u,v)
for k from 1 to |V|
for i from 1 to |V|
for j from 1 to |V|
if d[i][j] > d[i][k] + d[k][j]
d[i][j] ← d[i][k] + d[k][j]
end if
END
Status der Variablen:
| i | j | k |
| n.d. | n.d. | n.d. |
Beim Wechsel des Tabs wird die Aufgabe abgebrochen.
Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.
Prüfe dein Wissen: Wie würde der Algorithmus entscheiden?
BEGIN
for each vertex v
d[v][v] ← 0
for each edge (u,v)
d[u][v] ← w(u,v)
for k from 1 to |V|
for i from 1 to |V|
for j from 1 to |V|
if d[i][j] > d[i][k] + d[k][j]
d[i][j] ← d[i][k] + d[k][j]
end if
END
Status der Variablen:
| i | j | k |
Beim Wechsel des Tabs wird die Aufgabe abgebrochen.
Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.
Legende
 |
Knoten |
 |
Kante mit richtig eingetragenem Gewicht |
 |
Kante mit falsch eingetragenem Gewicht |
Legende
Welche Kosten haben die Kanten?
Du siehst gleich eine finale Matrix, die die günstigsten Pfadlängen zwischen allen Paaren von Knoten im gegebenen Graph darstellt. In dieser Aufgabe musst du die fehlende Kosten von Kanten bestimmen. Um die Kantenkost einzugeben, klicke doppelt auf die Kante und trage den Wert ein. Wenn du den richtigen Wert einträgst, wird die Kante grün gefärbt, ansonsten rot.
Entfernungen der Knoten:
| a | b | c | d | e | f | g | h | |
| a | 0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| b | 12 | 0 | 3 | 12 | 8 | 2 | 5 | 10 |
| c | 9 | 14 | 0 | 9 | 5 | 16 | 11 | 16 |
| d | 17 | 22 | 8 | 0 | 13 | 24 | 2 | 7 |
| e | 4 | 9 | 12 | 4 | 0 | 11 | 6 | 11 |
| f | 11 | 4 | 7 | 16 | 12 | 0 | 3 | 8 |
| g | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 0 | 5 |
| h | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 1 | 0 |
Welche Kosten haben die Kanten?
Hier siehst du in einer Tabelle, welche Entfernungen die Knoten voneinander haben.
Kannst du herausfinden, welche Kosten die Kanten haben? Klicke einfach doppelt auf eine Kante im Zeichenbereich und trage die Kosten ein, die diese Kante haben muss.
Beim Wechsel des Tabs wird die Aufgabe abgebrochen.
Du kannst die Anwendung in einem anderen Browserfenster öffnen, um parallel einen anderen Tab zu lesen.