Edmonds's Blossom Algorithm

Introduction
Create a graph
Run the algorithm
Description of the algorithm
More

Maximum matchings in general graphs

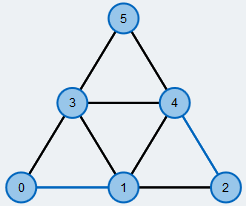
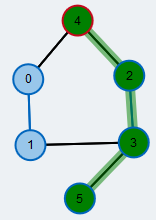
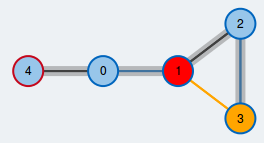
Maximum matching in a general graph.
Edges contained in the matching are colored blue.

An often occuring and well-studied problem in graph theory is finding a maximum matching in a graph \( G=(V,E)\). A matching M is a subset of edges such that every node is covered by at most one edge of the matching. M is a maximum matching if there is no other matching in G that has more edges than M.

This website is about Edmonds's Blossom Algorithm, an algorithm that computes a maximum matching in an undirected graph. In contrast to some other matching algorithms, the graph need not be bipartite. The algorithm was introduced by Jack Edmonds in 1965 and has been further improved since then. Many exact modern algorithms for the maximum matching problem on general graphs are still based on the ideas of the Blossom Algorithm.

Edmonds's Blossom Algorithm uses and extends the essential ideas of the Hopcroft-Karp algorithm, which computes a maximum matching for bipartite graphs. If you have not heard about this algorithm, we recommend having a look at it before proceeding with the Blossom Algorithm: Hopcroft-Karp Algorithm

We further assume that you are familiar with graph traversal, especially Breadth-First Search.

This website presents a visualization and detailed explanations of Edmonds's Blossom Algorithm. You can create a new graph, execute the algorithm on this graph to compute a maximum matching, and learn more about the theoretical backgrounds of the algorithm.

What do you want to do first?

SVG Download

Legend

	node
	undirected edge

Legend

Which graph do you want to execute the algorithm on?

Start with an example graph:

Select

Modify it to your desire:

To create a node, make a double-click in the drawing area.
To create an edge, first click on the output node and then click on the destination node.
Right-clicking deletes edges and nodes.

Download the modified graph:

Download

Upload an existing graph:

occured when reading from file:

the contents:

What next?

SVG Download

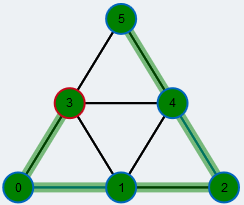
Legend

	yellow: free node
	red stroke: root of the BFS
	red: currently active node in BFS
	orange: currently checked neighbor in BFS
	green: node on the augmenting path
	large radius: contracted node
	orange: currently checked edge in BFS
	blue: matched edge
	grey overlay: edge in BFS tree
	green overlay: edge on the augmenting path

Legend

Algorithm status

rewind fast forward

Explanation
Pseudocode

Edmonds's Blossom Algorithm

The algorithm is ready to start now. Click "next" to execute a single step of the algorithm, "prev" to go one step back and "fast forward" for a fast execution of the algorithm.

Breadth-First Search finished

The BFS queue is empty. No augmenting path has been found by the modified Breadth-First Search.

Improved matching

The augmenting path is inverted to improve the matching. Inverting an augmenting path means that all unmatched edges along the path are changed to matched ones and vice versa. By doing so, the number of edges contained in the matching increases by 1. The new matching is colored blue.

Free vertices left

There are still unmatched vertices (yellow). We call them free vertices. We try to find an augmenting path to improve the matching. An augmenting path starts and ends at a free vertex and alternates between unmatched and matched edges.

Start Breadth-First Search

We pick one of the free vertices as the root node of a modified Breadth-First Search (BFS). Its stroke is colored red throughout the execution of the BFS. From the root node, we will construct a tree of alternating paths (BFS tree) until we reach another free vertex.

Pick next node from BFS queue

There are no neighbors left that we could check from the currently active node so we continue the BFS with the next node.

Contract blossom

The odd-length cycle we found is contracted to a single supernode. Supernodes are highlighted by a larger radius compared to the other nodes. We further push the new supernode to the BFS queue.

Continue BFS with next node

Pick the next node from the BFS queue. We call this node the currently active node and color it red. From this node, we will explore its neighbors to look for a free vertex.

Grow BFS tree

We add the neighbor and its mate to the BFS tree. The mate is further pushed to the BFS queue and we might continue our search from there later. The edges of the BFS tree are highlighted by a grey overlay.

Ignore even-length cycle

We can ignore even-length cycles. There is nothing to do in this case.

Check next neighbor

We check the next neighbor (orange) and find that it is already matched.

Check next neighbor

We check the next neighbor (orange edge) and find that it is a free vertex (yellow). Thus, there is an augmenting path between the root of the BFS and this vertex.

Check next neighbor

We check the next neighbor (orange) and find that this node is already contained in the BFS tree. Thus, there exists a cycle and we see that it has an odd number of edges. We call such a cycle a blossom.

Check next neighbor

We check the next neighbor (orange) and find that this node is already contained in the BFS tree. Thus, there exists a cycle and we see that it has an even number of edges.

Reconstruction of augmenting path

The augmenting path is highlighted green. Before improving the matching we have to expand the supernodes contained in the graph.

Expand supernodes

One of the supernodes is expanded and the augmenting path is adjusted correctly. There are still supernodes left that have to be expanded.

Reconstruction of augmenting path

The augmenting path from the BFS root to the free vertex found has been fully reconstructed and is highlighted green.

Reconstruction of augmenting path finished

After the expansion of all supernodes the augmenting path is fully reconstructed and highlighted green.

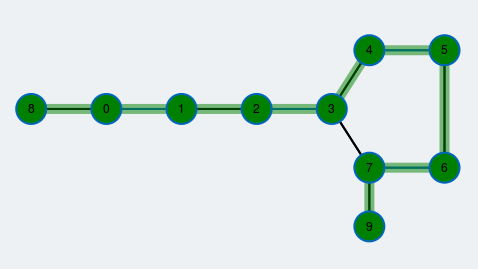
Algorithm finished

There are no free vertices in the graph anymore so we have found a matching of maximum cardinality. Its edges are colored blue.

BEGIN

WHILE F != ∅ DO (*set of free nodes F*)

pick r ∈ F

queue.push(r) (*BFS queue*)

T ← ∅ (*BFS tree T*)

T.add(r)

WHILE queue != ∅

v ← queue.pop()

FOR ALL neighbors w of v DO

IF w ∉ T AND w matched THEN

T.add(w)

T.add(mate(w))

queue.push(mate(w))

ELSE IF w ∈ T AND even-length

cycle detected THEN

CONTINUE

ELSE IF w ∈ T AND odd-length

cycle detected THEN

contract cycle

ELSE IF w ∈ F THEN

expand all contracted nodes

reconstruct augmenting path

invert augmenting path

END

If you switch tabs, the execution will be terminated.

You can open another browser window to read the description in parallel.

Matchings in graphs

Figure 1.
Matching in a non-bipartite graph which is not maximum. 3 and 5 are free vertices.

Figure 2.
Augmenting path from free vertex 3 to free vertex 5.

Figure 3.
Matching after inverting the augmenting path. Since there are no free vertices anymore, the matching must be maximum.

Figure 4.
Layered BFS tree (in grey) with root 8 and currently active node 3. Layer 0: 8, Layer 1: 0 and 2, Layer 2: 1 and 3, ...

We consider an undirected graph \( G=(V,E)\) with a set of vertices V and a set of edges E. A matching \(M \subseteq E\) is a subset of edges such that every vertex is covered by at most one edge of M. In Figure 1, we illustrate a valid matching in a graph. Its edges are colored blue. Each node is incident to at most one edge. If we added e.g. the edge between 0 and 3 to the current matching, the result would not be a matching anymore because 0 would then be contained twice in the matching.

We call a vertex that is not covered by the matching a free vertex. Given an edge \( e = \{v, w\} ∈ M\), v is the mate of w and vice versa. In our example, 3 and 5 are free vertices because they are not incident to any of the blue edges, 0 and 1 are mates of each other and 2 and 4 as well.

A matching M is called a maximum matching if its number of edges is maximum, i.e. if there does not exist any other matching M' in G with |M'|>|M|. The matching in Figure 1 is not maximum. We could evidently add the edge between the free vertices 3 and 5 to our matching and, by doing so, increase its number of edges to 3.

A graph is called bipartite if its vertices can be partitioned into two sets V₁ and V₂ such that every edge has one endpoint in V₁ and the other one in V₂. We know that a graph is bipartite if and only if it does not contain any odd cycles. Obviously, the graph in our example is not bipartite because it contains triangles.

Edmonds's Blossom Algorithm computes a maximum matching in a general graph. In contrast to many other algorithms, the graph is not required to be bipartite. It extends the idea of the Hopcroft-Karp Algorithm, which computes a maximum matching for a bipartite graph, by treating odd cycles appropriately.

Algorithm for bipartite graphs

We shortly recapitulate the basic concepts of the Hopcroft-Karp Algorithm that are also relevant for Edmonds's Blossom Algorithm. In order to improve a given matching, we try to find an augmenting path. An augmenting path is a path starting with a free node, ending with a free node and alternating between unmatched and matched edges. You can see an example of such an augmenting path (colored in green) in Figure 2. The path starts at the free vertex 3 and ends at the free vertex 5 and alternates between unmatched and matched edges. An other (trivial) example of an augmenting path would be the direct edge between 3 and 5 that we already considered in the first paragraph.

If we have found an augmenting path, we can improve the current matching by inverting the edges along the path: matched edges are changed to unmatched ones and vice versa. By doing so, we increase the cardinality of the matching by 1. The result of this procedure, a matching with three instead of two edges, can bee seen in Figure 3.

The following theorem by C. Berge is essential for the algorithm: A matching M is not maximum iff there exists an augmenting path in G. Thus, if we cannot find an augmenting path in G anymore, the resulting matching must be maximum.

But how can we find augmenting paths in a graph? We first pick an arbitrary free node r and start a modified Breadth-First Search (BFS) from there. While traversing the graph we construct a layered tree with root r. Edges from even to odd layers are unmatched edges, edges from odd to even layers are matched ones. Such a layered BFS tree is shown in Figure 4.

If we check a new node v during the execution of the BFS, one of the following cases may occur:

Case 1: v is a free node
Then we have found an augmenting path from r to v. We invert the path and are done with the BFS.
Case 2: v is already matched and not contained in the tree so far
Then we add v and its mate to the tree and push the mate of v to the BFS queue to continue the search from there later.
Case 3: v is already contained in the tree and we have detected a cycle of even length
There is nothing to do in this case, we ignore v and continue the BFS.
Case 4: v is already contained in the tree and we have detected a cycle of odd length
Since our graph is bipartite, this case cannot occur. When developing an algorithm for general graphs, however, we have to deal with this case as well.

General graphs: How to deal with odd-length cycles?

In general graphs, we also use the procedure explained above to find augmenting paths. However, we might detect odd-length cycles now (case 4) and have to treat this case appropriately. The idea is the following: We ignore the entire cycle by contracting it to a single supernode and continue the BFS in the new graph. When we have found an augmenting path at some point we have to expand all supernodes again (in reversed order) before inverting the matching. We call such odd-length cycles blossoms and this is why the algorithm is often referred to as the Blossom Algorithm.

We illustrate the procedure of contracting an odd-length cycle to a supernode and expanding it again with the following small example. In the picture to the left, we see a layered BFS tree with root 4. At the moment, the active node is 1 and we check the edge between 1 and 3. Since 3 is already contained in the tree, we know that there must be a cycle. The cycle has odd length, so we end up in case 4 and have to contract the whole blossom (1, 0, 4, 2, 3) to a new supernode 7 (on the right).

From 7 we continue the Breadth-First Search and find an augmenting path between 7 and 5. When we have found an augmenting path, we have to check if there are any contracted nodes that must be expanded again. Thus, we expand the supernode 7 to the original blossom (1, 0, 4, 2, 3) again (picture to the right). In addition, we have to reconstruct the augmenting path through the blossom correctly. Now that there are not any contracted nodes left we can invert the augmenting path.

Why does the shrinking method work?

We illustrate the idea behind the contraction of blossoms by having a look at the following example graph. The picture shows a snapshot of the algorithm: We have already constructed a layered tree with root 8 and now we are detecting the blossom (3,4,5,6,7) when exploring the edge between 5 and 6. We call the path from the root to the blossom (in this case 8 to 3) the stem and the intersecting node 3 the tip of the stem.

First note that the last edge of the stem must always be a matched edge (edge from 2 to 3 in the example). Then, for each node v contained in the blossom (except for the tip itself), there are two distinct paths from the tip to v. To reach node 6 from the tip, for instance, we could either traverse the blossom clockwise and choose the path (3,4,5,6) or we traverse it counter-clockwise and choose the path (3,7,6). One of the paths always ends with a matched edge, the other one with an unmatched edge. Thus, one of the two paths will make it possible to complete an augmenting path correctly later. At this point of the algorithm, however, we cannot make this decision because we do not know yet where the augmenting path (if there is any) will lead to. Thus, we postpone the decision of correctly traversing the blossom by shrinking the entire blossom to a supernode. When we find a free node, we expand the supernodes again and can reconstruct the augmenting path correctly.
Have a look at the two examples above. In both graphs, we find the free node 9 and have to reconstruct the path through the blossom. The edge from 9 to the blossom is unmatched in both cases so we have to start the traversal of the blossom with a matched edge (between 6 and 7). Thus, in the first graph, we go clockwise until we reach the tip 3 and in the second graph we go counter-clockwise. Suche

What now?

Create a graph and play through the algorithm

What is the pseudocode of the algorithm?


                    BEGIN
                      WHILE F != ∅ DO   (*set of free nodes F*)
                        pick r ∈ F
                        queue.push(r)             (*BFS queue*)
                        T ← ∅                    (*BFS tree T*)
                        T.add(r)
                        WHILE queue != ∅
                          v ← queue.pop()
                          FOR ALL neighbors w of v DO
                            IF w ∉ T AND w matched THEN
                              T.add(w)
                              T.add(mate(w))
                              queue.push(mate(w))
                            ELSE IF w ∈ T AND even-length cycle detected THEN
                              CONTINUE
                            ELSE IF w ∈ T AND odd-length cycle detected THEN
                              contract cycle
                            ELSE IF w ∈ F THEN
                              expand all contracted nodes
                              reconstruct augmenting path  
                              invert augmenting path
                    END

How fast is the algorithm?

Speed of algorithms

The speed of an algorithm is the total number of individual steps which are performed during the execution. Such individual steps might be assignments, comparisons or simple arithmetic operations.

Since it can be very difficult to count all individual steps, it is desirable to only count the approximate magnitude of the number of steps. This is also called the running time of an algorithm. Particularly, it is interesting to know the running time of an algorithm based on the size of the input (in this case the number of the vertices and the edges of the graph).

To denote the approximate running time of an algorithm, we use the so-called Big-Oh Notation. This allows us to ignore constant factors and lower-order terms. Instead of saying that the running time is exactly \( 2.5n^2 + 5n\log{n} - 1.5n + 8\), for instance, we often just say that the running time is in \( \mathcal{O} (n^2) \) because \( n^2 \) is the dominant term in this expression. For a more detailed explanation and a formal defintion of Big-Oh Notation as well as some easy techniques to analyze a piece of code, have a look e.g. here.

Running time of Edmonds's Blossom Algorithm

First of all, we would like to point out that there are a lot of different implementations of the Blossom Algorithm and they might significantly differ in their running time. Let n be the number of nodes and m the number of edges. The algorithm described in the original paper of Jack Edmonds [1] has a running time in \(\mathcal{O}(n^4)\). In the following paragraph we analyze the implementation based on Breadth-First Search which we used for this website. Its running time turns out to be \(\mathcal{O}(n^2 m)\). Using a more sophisticated implementation (by Micali and Vazirani, [3]), the running time can even be reduced to \(\mathcal{O}(\sqrt{n} m)\).

Analysis of the running time

There are at most n free nodes. For each of those nodes we execute a Breadth-First Search to find an augmenting path, which runs in \( \mathcal{O} (n+m) = \mathcal{O} (m) \) for connected graphs. In addition to the BFS, we have to perform at most n contractions (and thus at most n expansions). A single contraction (expansion) can be executed in time \( \mathcal{O} (m)\) because in the worst case we have to contract all nodes and edges to a single supernode. After having found an augmenting path, we have to invert it which takes time \( \mathcal{O} (n) \) in the worst case. All in all, this leads to a total running time of \( \mathcal{O} (n \cdot (m + nm + n)) = \mathcal{O} (n^2 m)\).

How can the algorithm be improved?

The algorithm on this website was implemented in a way that its basic ideas can be understood and visualized easily. Of course, there is much room to improve the performance of the algorithm. We present some ideas of Micali's and Vazirani's algorithm [3] which further reduce the running time to \(\mathcal{O}(\sqrt{n} m)\):

Instead of performing the BFS from a single free vertex we could start the BFS at all free vertices simultaneously. By doing so, we might find several disjoint augmenting paths at once and increase the cardinality of the matching by more than 1 with a single BFS.
Not all blossoms have to be shrinked immediately. There is a so-called blossoming condition that determines whether we have to contract an odd-length cycle or whether we may delay the shrinking.
A special labelling technique allows a fast expansion of blossoms.

Furthermore, Edmonds argues that - under certain circumstances - supernodes could be left contracted until their expansion is really needed. In our implementation, we expand all supernodes in the graph when finding an augmenting path but in many cases this is not necessary.

References

Literature

[1] Edmonds, Jack. "Paths, trees, and flowers." Canadian Journal of mathematics 17.3 (1965): 449-467.

[2] Edmonds, Jack. "Maximum matching and a polyhedron with 0, l-vertices." J. Res. Nat. Bur. Standards B 69.1965 (1965): 125-130.

[3] Micali, Silvio, and Vijay V. Vazirani. "An \(\mathcal{O}(\sqrt{|V|} |E|)\) algorithm for finding maximum matching in general graphs." Foundations of Computer Science, 1980., 21st Annual Symposium on. IEEE, 1980.

Web resources

[4] A Compendium of Applications of the Graph Matching Problem. http://www.cs.odu.edu/~mhalappa/matching/applications.html (accessed on June 6, 2016)

Where can I find more information about graph algorithms?

Other graph algorithms are explained on the Website of Chair M9 of the TU München.

Studying mathematics at the TU München answers all questions about graph theory (if an answer is known).

A last remark about this page's content, goal and citations

Chair M9 of Technische Universität München does research in the fields of discrete mathematics, applied geometry and the mathematical optimization of applied problems. The algorithms presented on the pages at hand are very basic examples for methods of discrete mathematics (the daily research conducted at the chair reaches far beyond that point). These pages shall provide pupils and students with the possibility to (better) understand and fully comprehend the algorithms, which are often of importance in daily life. Therefore, the presentation concentrates on the algorithms' ideas, and often explains them with just minimal or no mathematical notation at all.

Please be advised that the pages presented here have been created within the scope of student theses, supervised by Chair M9. The code and corresponding presentation could only be tested selectively, which is why we cannot guarantee the complete correctness of the pages and the implemented algorithms.

Naturally, we are looking forward to your feedback concerning the page as well as possible inaccuracies or errors. Please use the suggestions link also found in the footer.

To cite this page, please use the following information:

Title: Kruskal's Algorithm
Authors: Wolfgang F. Riedl, Johannes Feil; Technische Universität München
Link: https://www-m9.ma.tum.de/graph-algorithms/matchings-blossom-algorithm/index_en.html

Maximum matchings in general graphs

This website presents a visualization and detailed explanations of Edmonds's Blossom Algorithm. You can create a new graph, execute the algorithm on this graph to compute a maximum matching, and learn more about the theoretical backgrounds of the algorithm.

What do you want to do first?

Legend

Legend

Which graph do you want to execute the algorithm on?

Start with an example graph:

Modify it to your desire:

Download the modified graph:

Upload an existing graph:

What next?

Legend

Legend

Algorithm status

Edmonds's Blossom Algorithm

Breadth-First Search finished

Improved matching

Free vertices left

Start Breadth-First Search

Pick next node from BFS queue

Contract blossom

Continue BFS with next node

Grow BFS tree

Ignore even-length cycle

Check next neighbor

Check next neighbor

Check next neighbor

Check next neighbor

Reconstruction of augmenting path

Expand supernodes

Reconstruction of augmenting path

Reconstruction of augmenting path finished

Algorithm finished

If you switch tabs, the execution will be terminated.

Matchings in graphs

Algorithm for bipartite graphs

General graphs: How to deal with odd-length cycles?

Why does the shrinking method work?

What now?

Create a graph and play through the algorithm

What is the pseudocode of the algorithm?

How fast is the algorithm?

Speed of algorithms

Running time of Edmonds's Blossom Algorithm

Analysis of the running time

How can the algorithm be improved?

Related problems and algorithms

References

Literature

Web resources

Where can I find more information about graph algorithms?

A last remark about this page's content, goal and citations