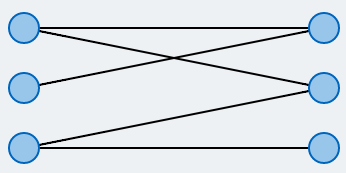
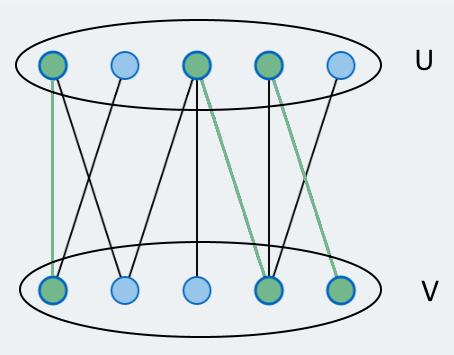
How big is the maximal matching?

Bipartite Matching

One possible application for the bipartite matching problem is allocating students to available jobs. The problem can be modeled using a bipartite graph: The students and jobs are represented by two disjunct sets of vertices. Edges represent possible assignments (based on qualifications etc). The goal is to find as many valid assignments as possible, such that each student can only take one job and each job can only be performed by a single student.

Let \( G=(V,E)\) be a given undirected graph. A subset \(M \subseteq E\) is called a matching, if no two edges in M share a node. A matching M is called maximal, if the cardinality of M is maximal amongst that of all matchings. In many real world problems, elements from multiple classes have to be assigned to one another. Whenever there are exactly two such classes, the problem is called bipartite matching.

Here we demonstrate the Hopcroft-Karp algorithm that solves the problem of finding maximal matchings on bipartite graphs.

What do you want to do first?

SVG Download

Legend

	Node
	Edge

Legend

Which graph do you want to execute the algorithm on?

Start with an example graph:

Select

Modify it to your desire:

The graph consists of two sets of vertices and edges between these sets.
To create a vertex in one of the sets, double click in the area of that set. You can create up to 8 nodes in each of the sets.
To create an edge, first click on the desired origin node and then on the desired destination node.
You can only create edges that run from one vertex-set to another.
Right clicking will delete vertices and edges.

Download the modified graph:

Download

Upload an existing graph:

occured when reading from file:

the contents:

What next?

SVG Download

Legend

	matched vertex
	matching edge

Legend

Current state of the algorithm

rewind fast forward

Explanation
Pseudocode

Initialization of the algorithm.

In the beginning, no vertex has a matching partner. Thus, the matching is empty.

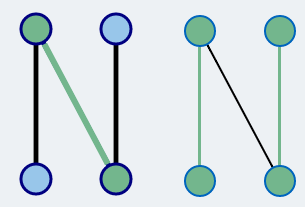
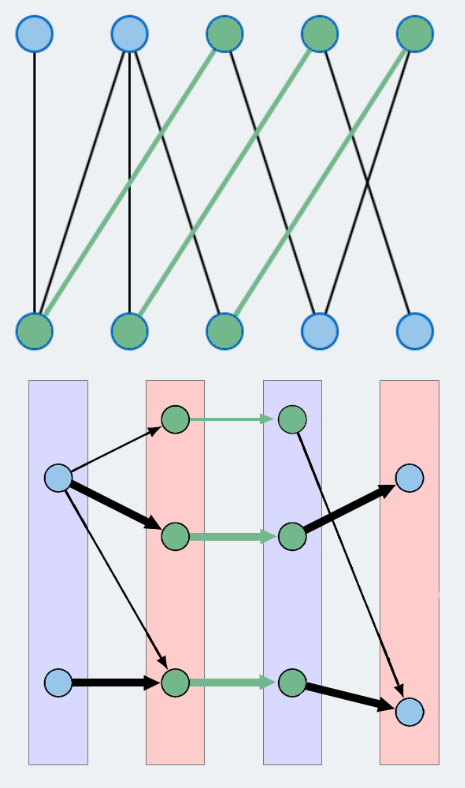
In each iteration, we look for an inclusion-maximal set of shortest vertex-disjunct augmenting paths.

An augmenting path is a path that starts in an unmatched node, ends in an unmatched node and alternates between edges outside of and inside the matching.

Inclusion-maximal means that no other path can be added to the set, such that the paths found stay vertex-disjunct (i.e. don't share any vertices).

When no further augmenting paths can be found, the current matching is optimal and the algorithm terminates..

BEGIN

M := ∅

REPEAT

l := Length of the shortest

augmenting path

Ρ := {P1,...,Pk} inklusion-maximal

set of vertex-disjunct

augmenting paths of lenght l

M := M ⊕ (P1 ∪ P2 ∪ ... ∪ Pk)

UNTIL Ρ = ∅

RETURN M

END

If you switch tabs, the execution will be terminated.

You can open another browser window to read the description in parallel.

Figure 1
Matching in a bipartite graph

Figure 2
Simple graph with an augmenting path.
On the left, an augmenting path has been highlightet. On the right, you see the graph after the augmentation.

Figure 3
Graph with its corresponding layered graph.
The vertex-disjunct augmenting paths are highlighted in the layered graph.

Figure 4
The gray vertices are already included in other shortest augmenting paths in this iteration. The highlighted agumentation path is vertex-disjunct to all of the gray nodes that are already in use.

Matching on bipartite Graphs

Numerous allocation problems can be modeled as bipartite matching problems. A simple example is the matching of students to open job positions. Not every assignment is possible as students will differ in their qualifications. The problem can be made easier to grasp if you consider the students to be a set of vertices and the jobs as another set of vertices. The edges between these sets will then represent all valid assignments of a student to a job. The goal is to find as many valid assignments as possible, while each student may only take one job and each job can be assigned to only a single student.

Let \(G=(V,E)\) be a given bipartite graph. A graph is called bipartite if it consists of two sets of vertices U and V, such that no edges exist within these sets. A matching is a set of edges, such that every vertex lies on at most one of the edges in this set. Figure 1 shows a matching in a bipartite graph. The problem we investigate is to find a mathching on G with maximal cardinality (i.e. maximal number of elements).

Idea of the Algorithm

Let M be the current matching (starting with the empty set). We will call an edge a matching edge if it is contained in M, and a free edge otherwise. In the illustrations, free and matching edges are shown in black and green, respectively. A node that lies on a matching edge is called covered (or matched). Otherwise the vertex is free. Covered nodes are shown in green, free nodes in blue. An augmenting path in the graph G is a path that

starts in a free node,
ends in a free node, and
alternates between free and matching edges.

Figure 2 illustrates an augmenting path in a graph.

Consider an augmenting path. If we remove all its matching edges from M, but add all its free edges, then the cardinality of M will increase by exactly 1. All nodes on the augmenting path lie on at most one matching edge. The end nodes of the path are not part of any matching edge, therefore we get a valid matching again after augmentation. The number of free edges in any augmenting path is exactly the number of matching edges plus 1. Thus the matching will be enlarged after augmentation.

A theorem in Graph Theory states the following:
A matching M in G(V,E) is maximal (w.r.t. cardinality) iff (if and only if) no augmenting paths exist.
A simple algorithm to find maximal matchings is thus to search for an augmenting path and increase the size of the matching along it. If no more augmenting paths can be found, the matching is optimal. However, the running time of this algorithm can be quite long in some cases.

The algorithm by Hopcroft and Karp improves the runtime when compared to the simple algorithm above. In each iteration, it only considers the shortest augmenting paths, and looks for a set of vertex-disjunct augmenting paths, i.e. no two such paths can share a node.

The set of shortest vertex-disjunct augmenting paths should be inclusion-maximal. This means that no other augmenting path exists that is vertex-disjunct to the paths already contained in the set. After finding the inclusion-maximal set of augmenting paths, we augment the matching and start a new iteration. After each iteration, the length of the shortest augmenting path will increase. The proof for this is somewhat complicated and will be ommitted here. However, it should be intuitive that the length of augmenting paths cannot become shorter after an augmentation. If no more augmenting paths exist, the algorithm terminates.

Finding Shortest Augmenting Paths

The shortest augmenting paths can be found using Breadth-first (BFS) und Depth-first search (DFS). We start with all free nodes in an (arbitrary) set of vertices and add these to the first layer of a layered graph, that will represent a decomposition of V into multiple layers and will be explained in more detail in the following. The layered graph will be created iteratively, until a free node has been found or all nodes have already been checked. The layered graph is constructed using the following procedure:

Starting from the nodes of the current layer one follows all edges to neighbors that haven't been considered yet. These neighbors make up the next layer of the graph. If this new layer contains a free node, the procedure will terminate; if the layer is empty, it will terminate as well and return that no further augmenting paths exist. Otherwise the layered graph will be extended by another layer, using the matching parners of the nodes in the previous layer. This layer of matching partners then becomes the current layer and the procedure is repeated until it terminates (see above). Finally, we end up with a layered graph that contains all (and only the) shortest augmenting paths, if any such paths exist.

The third figure shows a layered graph with four layers. The first layer consists of two free nodes from the vertex set above. Their neighbors are added to the second layer. Since none of the nodes in the second layer are free, a third layer is added, comprising the matching partners of the nodes in the second layer. All neighbors of this third layer that have not been considered yet are finally added to the fourth layer. As two of these vertices are free, the procedure ends after four layers.

Now, we use the layered graph from the last stet to find an inclusion-maximal set of vertex-disjunct augmenting paths. We use a Depth-first search starting with the free nodes in the first layer. If there is an augmenting path starting in one of these nodes, then it will be found. All nodes that are being used in this path will be deleted from the layered graph, or highlighted. While executing the algorithm, these nodes will be marked in gray. Applying this procedure to all nodes of the first layer, the set of shortest augmenting paths found this way will be vertex-disjunct, and after termination of the procedure no other augmenting paths will exist that is vertex-disjunct with respect to those already found.

In Figure three, the vertex-disjunct augmenting paths are highlighted by bold arrows. Thus, in this iteration the algorithm would augment the matching using these two augmenting paths. Afterwars a new iteration would begin and a new layered graph would be constructed.

The advantage of the layered graph is that all shortest augmenting paths can be found simultaneously. In the worst case, we have to check all edges in order to specify an inclusion-maximal set of shortest, vertex-disjunct augmenting paths.

What's next?

Create a graph and run the algorithm

Test your knowledge in the exercises

SVG Download

Legend

	matched vertex
	matching edge

Legend

Test your knowledge: What would the algorithm do?

Skip this question

Explanation
Pseudocode

BEGIN

M := ∅

REPEAT

l := length of the shortest

augmenting path

Ρ := {P1,...,Pk} inclusion-maximal

set of vertex-disjunct

augmenting paths of length l

M := M ⊕ (P1 ∪ P2 ∪ ... ∪ Pk)

UNTIL Ρ = ∅

RETURN M

END

In this part you can test your knowledge: What would the algorithm do?

The algorithm will be executed normally, but will stop in a few places. Then you will have to predict, what the algorithm would do next.

Hint: Recall the description of the algorithm.

If you switch tabs, the execution will be terminated.

You can open another browser window to read the description in parallel.

SVG Download

Legend

	matched vertex
	matching edge

Legend

Try finding augmenting paths yourself

Try finding augmenting paths yourself.

The Hopcroft-Karp algorithm uses augmenting'paths in order to find a maximal matching. In this exercise you will experiment with augmenting paths.

The algorithm will stop in some places. Then you will have to fill in an augmenting path. It is not necessary that you find the shortest augmenting path. You may choose any augmenting path you like.

Task is terminated if the tab is changed.

You can open another browser window for reading the description in parallel.

What's the (Pseudo-)Code of the algorithm?


                Input: Bipartite unweighted Graph G=(U ∪ V, E)
                Output: Matching M ⊆ E
                    BEGIN
                      M := ∅
                      REPEAT
                        l := length of the shortest augmenting paths
                        Ρ := {P1,...,Pk} inklusion-maximal set of
                             vertex-dijunct augmenting pathsl of length l
                        M := M ⊕ (P1 ∪ P2 ∪ ... ∪ Pk)
                      UNTIL Ρ = ∅
                      RETURN M
                    END

How fast is the algorithm?

Speed of algorithms

The speed of an algorithm is the total number of individual steps which are performed during the execution.

These steps are for example:

Assignments – Set distance of a node to 20.
Comparisons – Is 20 greater than 23?
Comparison and assignment – If 20 is greater than 15, set variable n to 20
Simple Arithmetic Operations – What is 5 + 5?

Since it can be very difficult to count all individual steps, it is desirable to only count the approximate magnitude of the number of steps. This is also called the running time of an algorithm. Particularly, it is interesting to know the running time of an algorithm based on the size of the input (in this case the number of the vertices and the edges of the graph).

Running time of the Hopcroft-Karp algorithmus

Assume the graph contains n vertices and m edges. In each iteration an inclusion-maximal set of shortest node-disjunct augmenting paths is found. Let M be a matching and M* the optimal matching. Then there are \( |M^*|-|M| \) vertex-disjunct augmenting paths with respect to M. Consider the symmetric difference M* ⊕ M = M*\M ∪ M\M*. Each node can lie on at most two edges (one in M* and one in M). Then the symmetric difference only contains vertex-disjunct circles and paths. In a circle, the number of edges from M is equal to that of edges from M*. But then there must exist \( |M^*|-|M| \) vertex-disjunct alternating paths, that contain more edges from M* than from M. These are exactly the augmenting paths with respect to M.

Let M be a matching an l the length of the shortest augmenting path with respect to M. Then the cardinality of the optimal Matchin is at most \( |M| + \frac{n}{(l+1)}\). There are \( |M^*|-|M| \) vertex-disjunct augmenting paths with respect to M. Each augmenting path has at least l+1 vertices, since the length of the shortest augmenting path is l. Then the following holds: \( (|M^*|-|M|)*(l+1) \leq n \), since the paths are vertex-disjunct and there are n nodes in the graph. Thus, \( |M^*|-|M| \leq \frac{n}{(l+1)}\) This means there are at most \( \frac{n}{(l+1)}\) possible augmentations with respect to M.

The length of the shortest augmenting path increases in each iteration. (This won't be proven here, a proof can be found in the literate.) Intuitively, however, it should be clear, that the augmenting paths cannot become shorter. But then after \(\sqrt{n}\) iterations of the algorithm, the length of the shortest augmenting path must be at least \(\sqrt{n}\). Then there are at most \(\frac{n}{\sqrt{n}+1} \leq \sqrt{n}\) additional augmentations. In each iteration, at least one augmenting paths ist found. Then it follows, that there can be at most \(2\sqrt{n}\) iterations before the algorithm terminates.

During execution of an interation, each edge is used a constant number of times. BFS and DFS are used, where each edge is only considered once. Furthermore, the matching is being updated. We can thus consider the processing of an edge in each iteration as a single execution step. Then every iteration can be executed in \(m\) steps. See "Description of the Algorithm" for details.
The total running time of the algorithm is then in the order of magnitude of \(m\sqrt{n}\).

How can we show that the algorithm always works correctly?

In each iteration of the algorithm it looks for augmenting paths and improves the matching. Only finitely many improvements can be made, thus the algorithm will always terminate. A theorem in Graph Theory states the follwing:
A matching M in G(V,E) is maximal by cardianality, if and only if there is no augmenting path. (Berge´s Lemma)
After the last iteration of the Hopcroft-Karp algorithm there are no more augmenting paths. Then the matching that has been found thus far must be optimal and the algorithm thus arrives at the correct result.

Where can I find more information on graph algorithms??

Other graph algorithms are explained on the Website of Chair M9 of the TU München.

Furthermore there is an interesting book about shortest paths: Das Geheimnis des kürzesten Weges

Studying mathematics at the TU München answers all questions about graph theory (if an answer is known).

A last remark about this page's content, goal and citations

Chair M9 of Technische Universität München does research in the fields of discrete mathematics, applied geometry and the mathematical optimization of applied problems. The algorithms presented on the pages at hand are very basic examples for methods of discrete mathematics (the daily research conducted at the chair reaches far beyond that point). These pages shall provide pupils and students with the possibility to (better) understand and fully comprehend the algorithms, which are often of importance in daily life. Therefore, the presentation concentrates on the algorithms' ideas, and often explains them with just minimal or no mathematical notation at all.

Please be advised that the pages presented here have been created within the scope of student theses, supervised by Chair M9. The code and corresponding presentation could only be tested selectively, which is why we cannot guarantee the complete correctness of the pages and the implemented algorithms.

Naturally, we are looking forward to your feedback concerning the page as well as possible inaccuracies or errors. Please use the suggestions link also found in the footer.

To cite this page, please use the following information:

Title: The Hopcroft-Karp Algorithm
Authors: Wolfgang F. Riedl, Ruslan Zabrodin; Technische Universität München
Link: https://www-m9.ma.tum.de/graph-algorithms/matchings-hopcroft-karp