

- Introduction
- Create a graph
- Run the algorithm
- Description of the algorithm
- Exercise 1
- Exercise 2
- More
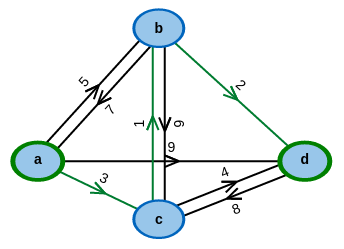
What are the cheapest paths between pairs of nodes?
Shortest Paths between all Pairs of Nodes
When considering the distances between locations, e.g. in logistics, one often encounters the problem of finding shortest paths. In such situations, the locations and paths can be modeled as vertices and edges of a graph, respectively.
In many problem settings, it's necessary to find the shortest paths between all pairs of nodes of a graph and determine their respective length. The Floyd-Warshall algorithm solves this problem and can be run on any graph, as long as it doesn't contain any cycles of negative edge-weight. Otherwise, those cycles may be used to construct paths that are arbitrarily short (negative length) between certain pairs of nodes and the algorithm cannot find an optimal solution.
This applet presents the Floyd-Warshall algorithm which finds shortest paths between all pairs of nodes.
What do you want to do first?
Which graph do you want to execute the algorithm on?
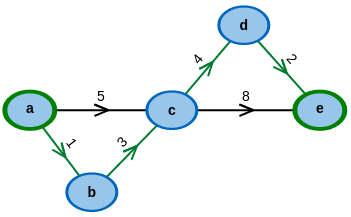
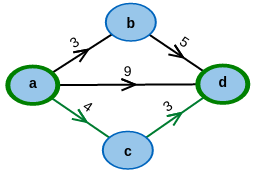
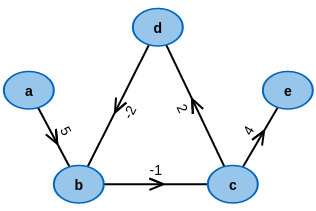
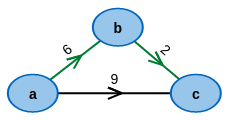
Start with an example graph:
Modify it to your desire:
- To create a node, make a double-click in the drawing area.
- To create an edge, first click on the output node and then click on the destination node.
- The edge weight can be changed by double clicking on the edge.
- Right-clicking deletes edges and nodes.
Download the modified graph:
DownloadUpload an existing graph:
What next?
Current state of the algorithm
BEGIN
FOR ALL v ∈ V
d[v][v] ← 0
FOR ALL (u,v) ∈ E
d[u][v] ← w(u,v)
for k from 1 to |V|
for i from 1 to |V|
for j from 1 to |V|
if d[i][j] > d[i][k] + d[k][j]
d[i][j] ← d[i][k] + d[k][j]
end if
END
Current state of variables:
| i | j | k |
| n.d. | n.d. | n.d. |
If you switch tabs, the execution will be terminated.
You can open another browser window to read the description in parallel.
Test your knowledge: How would the algorithm decide?
BEGIN
for each vertex v
d[v][v] ← 0
for each edge (u,v)
d[u][v] ← w(u,v)
for k from 1 to |V|
for i from 1 to |V|
for j from 1 to |V|
if d[i][j] > d[i][k] + d[k][j]
d[i][j] ← d[i][k] + d[k][j]
end if
END
Current state of the variables:
| i | j | k |
If you switch tabs, the execution will be terminated.
You can open another browser window to read the description in parallel.
What's the cost of the edges?
You will see a final matrix of shortest path lengths between all pairs of nodes in the given graph. In this exercise, your goal is to assign the missing weights to the edges. To enter a weight, double click the edge and enter the value. If you enter the correct value, the edge will be colored green, otherwise red.
Distances of the Nodes:
| a | b | c | d | e | f | g | h | |
| a | 0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| b | 12 | 0 | 3 | 12 | 8 | 2 | 5 | 10 |
| c | 9 | 14 | 0 | 9 | 5 | 16 | 11 | 16 |
| d | 17 | 22 | 8 | 0 | 13 | 24 | 2 | 7 |
| e | 4 | 9 | 12 | 4 | 0 | 11 | 6 | 11 |
| f | 11 | 4 | 7 | 16 | 12 | 0 | 3 | 8 |
| g | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 0 | 5 |
| h | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 1 | 0 |
What's the cost of the edges?
In this table you can see the distances between nodes.
Can you determine the missing costs of the edges? Simply double click on an edge in the drawing area and enter the correct cost.
If you switch tabs, you will lose all progress on the exercise.
You can open another browser window to read the description in parallel.