Introduction
Create a graph
Run the algorithm
Description of the algorithm
Exercise 1
Exercise 2
More

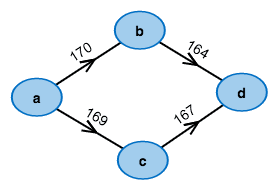
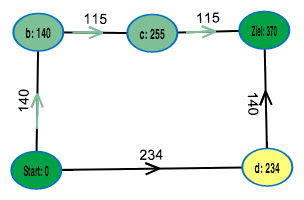
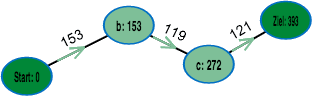
What's the cheapest way from left to right?

An informed search for the shortest path

You want to know, how to get from Munich to Frankfurt as fast as possible? Dijkstra's Algorithm can help you! But if you already know that Munich lies shouth of Frankfurt, this algorithm may be unnecessarily slow. Dijkstra's algorithm expands its search uniformly into all directions. It is, however, much faster to simply ignore most cities north of Frankfurt.

The A* algorithm was designed for these kinds of problems. It is similar to Dijkstra's algorithm, but its approach is much more goal-oriented. For the target node, Munich, it first computes an estimate of the shortest distance. Based on this estimate, it will achieve a fast computation

The A* algorithm can also compute the shortest distances between one city and all other cities. And the edges can describe costs, distances, or some other measure that is helpful for the user. It requires, however, that all edge costs (which is how we call the edge labels) must not be negative.

This applet presents the A* algorithm, which calculates the shortest path between two nodes in graphs with positive edge costs.

What do you want to do first?

SVG Download

Legend

	Node
	Edge with weight 50

Legend

Which graph do you want to execute the algorithm on?

Start with an example graph:

Modify it to your desire:

To create a node, make a double-click in the drawing area.
To create an edge, first click on the output node and then click on the destination node.
The edge weight is changed with a double-click on the edge.
Right-clicking deletes edges and nodes.

Download the modified graph:

Download

Upload an existing graph:

occured when reading from file:

the contents:

What next?

SVG Download

Legend

	Starting node from where the shortest path to the target is computed.
	Target node, towards whom the shortest path is computed.
	Node that has already been processed
	Node being processed.
	Node in the priority queue.
	"Predecessor edge" that is used by the shortest path to the node.

Legend

Algorithm status

rewind fast forward

Explanation
Pseudocode

BEGIN

d(v[1]) ← 0, parent(v[1]) ← v[1]

FOR i = 2,..,n DO

d(v[i]) ← ∞, parent(v[i]) ← NULL

h(v[i]) ← √(Σ(v[i].coord-ziel.coord)²)

queue.insert(v[1],0)

WHILE queue ≠ ∅ DO

u = queue.extractMin()

IF u == ziel DO RETURN "Path found!"

FOR ALL (u,w) ∈ E DO

dist ← d(u) + l(u,w)

IF w ∈ queue AND d(w) > dist DO

d(w) = dist, f = dist + h(u)

parent(w) = u

ELSE IF parent(w) == NULL THEN

d(w) = dist, f = dist + h(u)

parent(w) = u, queue.insert(w,f)

RETURN "Target unreachable"

END

Priority Queue:

Task is terminated if the tab is changed.

You can open another browser window for reading the description in parallel.

What's the shortest path from left to right?

Algorithm idea

The A* algorithm computes the shortest path between two nodes in a graph. If all shortest paths starting at some node are needed (which is what Dijkstra's Algorithm computes), the algorithm must be executed multiple times.

The A* algorithm is an informed search procedure. While Dijkstra's algorithm blindly chooses the next node available, the A* algorithm uses extra information to choose the best node leading to the target.

As additional information, the algorithm uses a heuristic that estimates the distance from any node to the target. This estimate acts as a rule of thumb for the algorithm and speeds up the computation.

Description of the algorithm

Kante vor Update — This edge is a shortcut.
We know that getting to the node on the left costs 20 units. The path from the left to the right node costs 1 unit.

During the A* algorithm, each node has one of the three following states:

The node is unknown: The node has not been processed yet and no way from the start to this node is known.
The node is in the priority queue: We know some way leading to this node, but there may be a shorter way.
The node is fully processed: We know the shortest path from the starting node to it.

The algorithm first adds the starting node to the empty priority queue. Each node in the priority queue has an f-value. This value is the sum of the distance from the starting node to this node and the estimate of its distance to the target node. The node with the smallest f-value leads the priority queue and will be processed next.

The algorithm now takes the node with the minimum f-value from the priority queue until the queue is empty or a path to the target node has been found. If the node taken from the queue is the target node, then the algorithm has found the shortest path and terminates. If the priority queue becomes empty, then no path from the start to the target is possible and the algorithm terminates.

After processing a node from the priority queue, its neighbors are inspected. The algorithm distinguishes three cases:

The neighbor has already been processed:
Then the algorithm does nothing.
The neighbor is already in the prioity queue:
If the current path is a shortcut, update its f-value.
The neighbor is not in the priority queue:
Compute the f-value of the node and add it to the priority queue.

Shortest paths to all nodes that have been found by the algorithm can be constructed via the procedure described below.

What is an admissible estimate function?

Recall the definition of the f-value: It is the sum of the distance of the node to the starting node and the estimated distance of the node to the target. The distance of the node to the starting node has already been computed. The estimated distance is given by some estimate function.

One possible estimate function is the straight line distance between two nodes. Mathematically, this is the euclidean distance between the nodes. If one node has the (real-world) coordinates (x₁, y₁), while the other node has corrdinates (x₂, y₂), their euclidean distance is √((x₁-x₂)²+(y₁-y₂)²).

The algorithm works with other estimate functions as well. However, these functions must be admissible. An estimate function is admissible, if it cannot overestimate the distance between two nodes. For example, if towns A and B are 10 km away from each other, then the estimate of their distance must be at least 10 km. If the estimate function is not admissible, the algorithm might give an incorrect solution.

Graph with distances — The green path from the starting node to node b is the cheapest path. It uses 3 edges.

Construction of the shortest path

Each time when updating the cost of some node, the algorithm saves the edge that was used for the update as the predecessor of the node.

At the end of the algorithm, the shortest path to each node can be constructed by going backwards using the predecessor edges until the starting node is reached.

If a node cannot be reached from the starting node, then its cost stays infite.

What now?

Create a graph and play through the algorithm

Test your knowledge in the exercises

SVG Download

Legend

	Starting node from where the shortest path to the target is computed.
	Target node, towards whom the shortest path is computed.
	Node that has already been processed
	Node being processed.
	Node in the priority queue.
	"Predecessor edge" that is used by the shortest path to the node.

Legend

Exercise: How does Dijkstra's algorithm work on a grid?

rewind Forward: Next question

Explanation
Pseudocode

BEGIN

d(v[1]) ← 0

FOR i = 2,..,n DO

d(v[i]) ← ∞, parent(v[i]) ← NULL

WHILE queue ≠ ∅ DO

u = queue.extractMin()

FOR ALL (u,w) ∈ E DO

dist ← d(u) + l(u,w)

IF w ∈ queue AND d(w) > dist DO

d(w) = dist, parent(w) = (u,w)

ELSE IF parent(w) == NULL THEN

d(w) = dist, parent(w) = (u,w)

queue.insert(w,dist)

END

Task is terminated if the tab is changed.

You can open another browser window for reading the description in parallel.

SVG Download

Legend

	Starting node from where the shortest path to the target is computed.
	Target node, towards whom the shortest path is computed.
	Node that has already been processed
	Node being processed.
	Node in the priority queue.
	"Predecessor edge" that is used by the shortest path to the node.

Legend

Exercise: How does the A* algorithm work on a grid?

rewind Forward: Next question

Explanation
Pseudocode

BEGIN

d(v[1]) ← 0, parent(v[1]) ← v[1]

FOR i = 2,..,n DO

d(v[i]) ← ∞, parent(v[i]) ← NULL

h(v[i]) ← √(Σ(v[i].coord-ziel.coord)²)

WHILE queue ≠ ∅ DO

u = queue.extractMin()

IF u == ziel DO RETURN "Path found"

FOR ALL (u,w) ∈ E DO

dist ← d(u) + l(u,w)

IF w ∈ queue AND d(w) > dist DO

d(w) = dist, f = dist + h(u)

parent(w) = u

ELSE IF parent(w) == NULL THEN

d(w) = dist, f = dist + h(u)

parent(w) = u, queue.insert(w,f)

RETURN "Target not reachable"

END

Task is terminated if the tab is changed.

You can open another browser window for reading the description in parallel.

What is the pseudocode of the algorithm?

Input: Weighted, directed or undirected graph G=(V,E) 
       using poisitive weight function l, starting node, target node.
Output: Shortest path between start and target node.


BEGIN
  d(start) ← 0, parent(start) ← start
  FOR i = 2,..,n DO
    d(v[i]) ← ∞, parent(v[i]) ← NULL
    h(v[i]) ← √((v[i].x-ziel.x)² + (v[i].y-ziel.y)²)
  queue.insert(start, 0)
  WHILE queue ≠ ∅ DO
    u = queue.extractMin()
    IF u == ziel DO 
      getPath()
      RETURN "Path found"
    FOR ALL (u,w) ∈ E DO
      dist ← d(u) + l(u,w)
     IF w ∈ queue AND d(w) > dist DO
       d(w) = dist, f = dist + h(u)
       parent(w) = u
     ELSE IF parent(w) == NULL THEN
       d(w) = dist, f = dist + h(u)
       parent(w) = u, queue.insert(w,f)
  RETURN "Target not reachable"
END


getPath():
BEGIN
 node ← ziel
 WHILE parent(node) != start DO
   path.add(node)
   node ← parent(node)
 path.add(start)
 invert(path)
 RETURN path
END

As the shortest path is constructed backwards (starting from the target), one must call the inversion function that inverts the order of the nodes. This gives the path in the correct order from start to target.

How fast is the algorithm?

Speed of algorithms

The speed of an algorithm is the total number of individual steps which are performed during the execution.

These steps are for example:

Assignments – Set distance of a node to 20.
Comparisons – Is 20 greater than 23?
Comparison and assignment – If 20 is greater than 15, set variable n to 20
Simple Arithmetic Operations – What is 5 + 5?

Since it can be very difficult to count all individual steps, it is desirable to only count the approximate magnitude of the number of steps. This is also called the running time of an algorithm. Particularly, it is interesting to know the running time of an algorithm based on the size of the input (in this case the number of the vertices and the edges of the graph).

Running time of the A* algorithm

When analyzing the running time of an algorithm, one usually considers the worst-case scenario fro this algorithm. This, however, is not very helpful for the A* algorithm, as its running time depends on the quality of the estimate function. In the worst case, the estimates are not helpful and the running time is the same as the running time of Dijkstra's algorithm.

Assume that the A* algorithm is run on a graph with n nodes and m edges.

Inspecting each node of the graph takes n steps.

We must extract the nodes from the priority queue before inspecting them. As extract the minimum from the priority queue n times,we need at most n · n steps for this.

Nodes are added to the priority queue, when the edges leaving some node are inspected. Based on the edge weight, the cost of nodes in the priority queue might be reduced. The algorithm therefor inspects all edges that can be reached from the starting node. This requires another m steps.

The overall running time of the algorithm, is therefore of order m + n², is we use simple list as the priority queue.

It is possible to improve the running time to m + n · log(n). This requires a more sophisticated data structure for storing the priority queue (e.g. a heap).

What are the differences to Dijkstra's algorithm?

Dijkstra's algorithm and the A* algorithm are very similar. As seen above, their running time might be identical if the estimate function is not helpful.

When should I use the A* algorithm?

The formal running time is only an estimate for the worst-case. If the A* algorithm has a good estimate function, its running time may be considerable lower than Dijkstra's algorithm's. You may have seen in the exercises that the A* algorithm must visit much less nodes than Dijkstra's algorithm. Therefore, Dijkstra's algorithm should be used if a good estimate function exists.

When should I use the Dijkstra's algorithm?

Dijkstra's algorithm can be considered a special case of the A* algorithm. If the estimate function is constant at 0 for each node, then the two algorithms are equal.

There exist applications, where no good estimate functions are available. Sometimes, it is unclear in which direction the target lies. For example, when searching for the next gas station, it is not clear from the start in which direction the search should go. In this case, Dijkstra's algorithm is a better choice.

Where can I find more information about graph algorithms?

Other graph algorithms are explained on the Website of Chair M9 of the TU München.

Furthermore there is an interesting book about shortest paths: Das Geheimnis des kürzesten Weges

Studying mathematics at the TU München answers all questions about graph theory (if an answer is known).

A last remark about this page's content, goal and citations

Chair M9 of Technische Universität München does research in the fields of discrete mathematics, applied geometry and the mathematical optimization of applied problems. The algorithms presented on the pages at hand are very basic examples for methods of discrete mathematics (the daily research conducted at the chair reaches far beyond that point). These pages shall provide pupils and students with the possibility to (better) understand and fully comprehend the algorithms, which are often of importance in daily life. Therefore, the presentation concentrates on the algorithms' ideas, and often explains them with just minimal or no mathematical notation at all.

Please be advised that the pages presented here have been created within the scope of student theses, supervised by Chair M9. The code and corresponding presentation could only be tested selectively, which is why we cannot guarantee the complete correctness of the pages and the implemented algorithms.

Naturally, we are looking forward to your feedback concerning the page as well as possible inaccuracies or errors. Please use the suggestions link also found in the footer.

To cite this page, please use the following information:

Title: The A*-algorithm
Authors: Melanie Herzog, Wolfgang F. Riedl, Lisa Velden; Technische Universität München
Link: https://www-m9.ma.tum.de/graph-algorithms/spp-a-star